多重指標
多重指標
一個n -維 多重指標是一個由整數構成的向量
多重指標
多重指標
設 為多重指標,定義:
多重指標
多重指標
多重指標
應用最廣的是非負的多重指標,此時可以定義:
多重指標
多重指標
多重指標
(假設)
多重指標
多重指標
設 定義
多重指標
多重指標
其中
多重指標
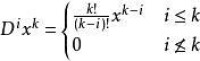
多重指標
命題:若i,k是非負的n維多重指標,且 則
按定義直接操作即可證明。
多重指標可以將單變元微積分的許多結果直接推廣到多變元。以下是幾個例子:
多元冪級數:有兩個以上變元的冪級數通常寫成
多重指標
多重指標
多重指標
其中 是n-維多元指標而,以簡化冗長的表法
多重指標
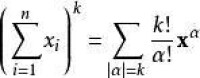
多重指標
多重指標
萊布尼茨公式:設 存在夠高階的導數,則
多重指標
多重指標
泰勒展開式:對一多元解析函數 f,當
充分小時有下述展開
多重指標
對於存在夠高階導數的函數,我們也有帶余項的泰勒展開式:
多重指標
多重指標
多重指標
多重指標
分部積分:對有界定義域 上的緊支集光滑函數,我們有
多重指標