共找到2條詞條名為通道容量的結果 展開
- 通道容量
- 傳信率
通道容量
通道容量
通道能無錯誤傳送的最大信息率。對於只有一個信源和一個信宿的單用戶通道,它是一個數,單位是比特每秒或比特每符號。它代表每秒或每個通道符號能傳送的最大信息量,或者說小於這個數的信息率必能在此通道中無錯誤地傳送。對於多用戶通道,當信源和信宿都是兩個時,它是平面上的一條封閉線,如圖中的OC1ABC2O。坐標R1和R2分別是兩個信源所能傳送的信息率,也就是R1和R2落在這封閉線內部時能無錯誤地被傳送。當有m個信源和信宿時,通道容量將是m維空間中一個凸區域的外界“面”。

通道容量
①恆參通道(平穩通道):通道的統計特性不隨時間變化。衛星通信通道在某種意義下可以近似為恆參通道。
②隨參通道(非平穩通道):通道的統計特性隨時間變化。如短波通信中,其通道可看成隨參通道
通道容量是通道的一個參數,反映了通道所能傳輸的最大信息量,其大小與信源無關。對不同的輸入概率分佈,互信息一定存在最大值。我們將這個最大值定義為通道的容量。一但轉移概率矩陣確定以後,通道容量也完全確定了。儘管通道容量的定義涉及到輸入概率分佈,但通道容量的數值與輸入概率分佈無關。我們將不同的輸入概率分佈稱為試驗信源,對不同的試驗信源,互信息也不同。其中必有一個試驗信源使互信息達到最大。這個最大值就是通道容量。
通道容量有時也表示為單位時間內可傳輸的二進位位的位數(稱通道的數據傳輸速率,位速率),以位/秒(b/s)形式予以表示,簡記為bps。
通信的目的是為了獲得信息,為度量信息的多少(信息量),我們用到了熵這個概念。在信號通過通道傳輸的過程中,我們涉及到了兩個熵,發射端處信源熵——即發端信源的不確定度,接收端處在接收信號條件下的發端信源熵——即在接收信號條件下發端信源的不確定度。接收到了信號,不確定度小了,我們也就在一定程度上消除了發端信源的不確定性,也就是在一定程度上獲得了發端信源的信息,這部分信息的獲取是通過通道傳輸信號帶來的。如果在通信的過程中熵不能夠減小(不確定度減小)的話,也就沒有通信的必要了。最理想的情況就是在接收信號條件下信源熵變為0(不確定度完全消失),這時,發端信息完全得到。
通信通道,發端X,收端Y。從信息傳輸的角度看,通過通道傳輸了I(X;Y)=H(X)-H(X|Y),(接收Y前後對於X的不確定度的變化)。I該值與兩個概率有關,p(x),p(y|x),特定通道轉移概率一定,那麼在所有p(x)分佈中,max I(X;Y)就是該通道的通道容量C(互信息的上凸性)。
圖2
圖3
通道是由輸入集A、輸出集B和條件概率P(y│x),y∈B,x∈A所規定的。當B是離散集時,歸一性要求就是(圖1)當B是連續集時,P(y│x)應理解為條件概率密度,上式就成為積分形式。如A和B都是離散集,通道所傳送的信息率(每符號)就是輸出符號和輸入符號之間的互信息(圖2)
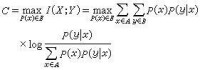
圖4
當A或B是連續集時,相應的概率應理解為概率密度,求和號應改為積分,其他都相仿。
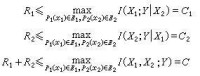
圖5
圖6
要使通道容量有確切的含義,尚須證明相應的編碼定理,就是說當信息率低於通道容量時必存在一種編碼方法,使之在通道中傳輸而不發生錯誤或錯誤可任意逼近於零。已經過嚴格證明的只有無記憶單用戶通道和多用戶通道中的某些多址接入通道和退化型廣播通道。對某些有記憶通道,只能得到容量的上界和下界,確切容量尚不易規定。
通道的輸入、輸出都取值於離散符號集,且都用一個隨機變數來表示的通道就是離散單符號通道。由於通道中存在干擾,因此輸入符號在傳輸中將會產生錯誤,這種通道干擾對傳輸的影響可用傳遞概率來描述。
通道傳遞概率通常稱為前向概率。它是由於通道雜訊引起的,所以通常用它描述通道雜訊的特性。
有時把p(x)稱為輸入符號的先驗概率。而對應的把p(x|y)稱為輸入符號的后驗(後向)概率。
平均互信息I(X;Y)是接收到輸出符號集Y后所獲得的關於輸入符號集X的信息量。信源的不確定性為H(X),由於干擾的存在,接收端收到Y后對信源仍然存在的不確定性為H(X|Y),又稱為通道疑義度。信宿所消除的關於信源的不確定性,也就是獲得的關於信源的信息為I(X;Y),它是平均意義上每傳送一個符號流經通道的信息量,從這個意義上來說,平均互信息又稱為通道的信息傳輸率,通常用R表示。
有時我們所關心的是通道在單位時間內平均傳輸的信息量。如果平均傳輸一個符號為t秒,則通道平均每秒鐘傳輸的信息量為Rt一般稱為信息傳輸速率。
對於固定的通道,總存在一種信源(某種輸入概率分佈),使通道平均傳輸一個符號接收端獲得的信息量最大,也就是說對於每個固定通道都有一個最大的信息傳輸率,這個最大的信息傳輸率即為通道容量,而相應的輸入概率分佈稱為最佳輸入分佈。
通道容量是通道傳送信息的最大能力的度量,通道實際傳送的信息量必然不大於通道容量。
要使通道容量有確切的含義,尚須證明相應的編碼定理,就是說當信息率低於通道容量時必存在一種編碼方法,使之在通道中傳輸而不發生錯誤或錯誤可任意逼近於零。已經過嚴格證明的只有無記憶單用戶通道和多用戶通道中的某些多址接入通道和退化型廣播通道。對某些有記憶通道,只能得到容量的上界和下界,確切容量尚不易規定。

圖7 通道容量
對於其他通道的容量計算曾提出過一些方法,但都有較多的限制。比較通用的解法是迭代計算,可藉助計算機得到較精確的結果。
對於連續通道,只需把輸入集和輸出集離散化,就仍可用迭代公式來計算。當然如此形成的離散集,包含的元的數目越多,精度越高,計算將越繁。對於資訊理論中的其他量,如信息率失真函數,可靠性函數等,都可以用類似的方法得到的各種迭代公式來計算。
從求通道容量的問題實際上是在約束條件下求多元函數極值的問題,在通常情況下,計算量是非常大的。下面我們介紹一般離散通道的平均互信息達到通道容量的充要條件,在某些情況下它可以幫助我們較快地找到極值點。(定理略去)
通道容量定理只給出了達到通道容量時,最佳輸入概率分佈應滿足的條件,並沒有給出最佳輸入概率分佈值,也沒有給出通道容量的數值。另外,定理本身也隱含著達到通道容量的最佳分佈不一定是唯一的,只要輸入概率分佈滿足充要條件式,就是通道的最佳輸入分佈。在一些特殊情況下,我們常常利用這一定理尋求輸入分佈和通道容量值。
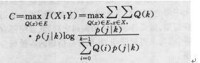
圖8
對於連續通道,應將式中概率分佈換成概率密度,求和號換成積分號,即得出連續通道的容量公式。
圖9
通道容量
通道容量
容量的計算是在特定約束條件下,求傳信率函數I(X;Y)的極大值問題。對離散通道的約束條件是輸入符號的概率,對於連續通道,除了概率約束條件外,還可有不同的約束條件,如平均功率或峰值功率受限。由於I(X;Y)是輸入分佈(或密度)的上凸函數,故其極值即為最大值,可見,求容量在於求I(X;Y)的條件極值。簡單情況下,離散通道可用拉格朗日乘子法求解,連續通道可用變分法求解。R.E.勃拉赫特提出的迭代演演算法可精確求解一般離散無記憶通道的容量,也可用來近似計算連續通道的容量以及率失真函數和可靠性函數。
圖10
通道容量
通道容量
常見的二元對稱通道(BSC)的容量公式如圖,式中ε是符號出差錯的概率。常見的加性白高斯雜訊(AWGN)通道的容量公式如圖,式中S是通道允許的平均功率,N0是白高斯雜訊的單邊功率譜密度,F是通道許用帶寬。當F→∞時有。令Eb表示每比特信息佔有的能量,則S=REb,R是傳信率。由圖及編碼定理有,通稱-1.6dB為仙農極限,它表示在無限帶寬的AWGN通道中,傳送1bit信息所需的最小Eb/N0。
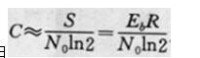
圖11
實際離散通道的輸入和輸出常常是隨機變數序列,用隨機矢量來表示,稱為離散多符號通道。
若在任意時刻通道的輸出只與此時刻通道的輸入有關,而與其他時刻的輸入和輸出無關,則稱之為離散無記憶通道,簡稱為DMC(discrete memoryless channel)。
輸入、輸出隨機序列的長度為N的離散無記憶平穩通道通常稱為離散無記憶通道的N次擴展通道。
對於離散無記憶N次擴展通道,當信源是平穩無記憶信源時,其平均互信息等於單符號通道的平均互信息的N倍。
當信源也是無記憶信源並且每一時刻的輸入分佈各自達到最佳輸入分佈時,才能達到這個通道容量NC。
前面我們分析了單符號離散通道和離散無記憶通道的擴展通道。實際應用中常常會遇到兩個或更多個通道組合在一起使用的情況。例如,待發送的消息比較多時,可能要用兩個或更多個通道并行發送,這種組合通道稱為並聯通道;有時消息會依次地通過幾個通道串聯發送,例如無線電中繼通道,數據處理系統,這種組合通道稱為級聯通道。在研究較複雜通道時,為使問題簡化,往往可以將它們分解成幾個簡單的通道的組合。這一節我們將討論這兩種組合通道的通道容量與其組成通道的通道容量之間的關係。
獨立並聯通道的通道容量才等於各通道容量之和。
級聯通道是通道最基本的組合形式,許多實際通道都可以看成是其組成通道的級聯。兩個單符號通道組成的最簡單的級聯通道X→Y→Z組成一個馬爾可夫鏈。根據馬爾可夫鏈的性質,級聯通道的總的通道矩陣等於這兩個串接通道的通道矩陣的乘積。求得級聯通道的總的通道矩陣后,級聯通道的通道容量就可以用求離散單符號通道的通道容量的方法計算。
數字通道是一種離散通道,它只能傳送離散值的數字信號,通道的帶寬決定了通道中能不失真的傳輸脈序列的最高速率。
