共軛

兩個實部相等，虛部互為相反數的複數互為共軛複數(conjugatecomplexnumber)。（當虛部不等於0時也叫共軛虛數）複數z的共軛複數記作（z上加一橫，英文中可讀作Conjugatez,zconjugateorzbar），有時也可表示為。

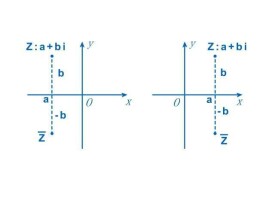
根據定義，若z=a+ib(a，b∈R)，則=a－ib（a,b∈R)。在複平面上，共軛複數所對應的點關於實軸對稱。（如右圖）

當都是有理根式，而、中至少有一個是無理根式時，稱和互為“共軛根式”。由平方差公式，這兩式的積為有理式

以已知雙曲線的虛軸為實軸，實軸為虛軸的雙曲線叫做原雙曲線的共軛雙曲線，如雙曲線H：與雙曲線H'：叫做一對共軛雙曲線(a>0,b>0)。

主要性質有：它們有共同的漸近線，它們的四個焦點共圓，它們的離心率的倒數的平方和等於1。

共軛矩陣又稱Hermite陣。Hermite陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。

把矩陣轉置后，再把每一個數換成它的共軛複數。

水躍中，躍前水深與躍后水深的互稱或共稱。

在構造地質學中存在共軛剪節理

兩向量間的一種特殊關係。設A為n×n對稱正定矩陣，向量p，p∈R.若滿足條件(p)Ap=0，則稱p和p關於A是共軛方向，或稱p和p關於A共軛。一般地，對於非零向量組p，p，…，p∈R，若滿足條件：(p)Ap=0(i≠j，i，j=1，2，…，n)，則稱該向量組關於A共軛。

以一組共軛方向作為搜索方向來求解無約束非線性規劃問題的一類下降演演算法。是在研究尋求具有對稱正定矩陣Q的n元二次函數

最優解的基礎上提出的一類梯度型演演算法，包含共軛梯度法和變尺度法。根據共軛方向的性質，依次沿著對Q共軛的一組方向作一維搜索，則可保證在至多n步內獲得二次函數的極小點。共軛方向法在處理非二次目標函數時也相當有效，具有超線性的收斂速度，在一定程度上克服了最速下降法的鋸齒形現象，同時又避免了牛頓法所涉及的海色(Hesse)矩陣的計算和求逆問題。對於非二次函數，n步搜索並不能獲得極小點，需採用重開始策略，即在每進行n次一維搜索之後，若還未獲得極小點，則以負梯度方向作為初始方向重新構造共軛方向，繼續搜索。