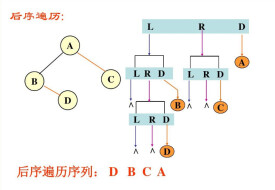
後序遍歷

後序遍歷首先遍歷左子樹，然後遍歷右子樹，最後訪問根結點，在遍歷左、右子樹時，仍然先遍歷左子樹，然後遍歷右子樹，最後遍歷根結點。即：

若二叉樹為空則結束返回，

否則： （1）後序遍歷左子樹

（2）後序遍歷右子樹

（3）訪問根結點

如右圖所示二叉樹

後序遍歷結果：DEBFCA

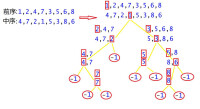
已知前序遍歷和中序遍歷，就能確定後序遍歷。

首先要搞清楚先序、中序、後序的非遞歸演演算法共同之處：用棧來保存先前走過的路徑，以便可以在訪問完子樹后，可以利用棧中的信息，回退到當前節點的雙親節點，進行下一步操作。

後序遍歷的非遞歸演演算法是三種順序中最複雜的，原因在於，後序遍歷是先訪問左、右子樹，再訪問根節點，而在非遞歸演演算法中，利用棧回退到時，並不知道是從左子樹回退到根節點，還是從右子樹回退到根節點，如果從左子樹回退到根節點，此時就應該去訪問右子樹，而如果從右子樹回退到根節點，此時就應該訪問根節點。所以相比前序和後序，必須得在壓棧時添加信息，以便在退棧時可以知道是從左子樹返回，還是從右子樹返回進而決定下一步的操作。