總統證法
總統證法
學過幾何的人都知道勾股定理。它是幾何中一個比較重要的定理,應用十分廣泛。迄今為止,關於勾股定理的證明方法已有600餘種。其中,美國第二十任總統伽菲爾德的證法在數學史上被傳為佳話。
伽菲爾德總統為什麼會想到去證明勾股定理呢?難道他是數學家或數學愛好者?答案是否定的。事情的經過是這樣的:
在1876年一個周末的傍晚,在美國首都華盛頓的郊外,有一位中年人正在散步,欣賞黃昏的美景,他就是當時美國俄亥俄州共和黨議員伽菲爾德。他走著走著,突然發現附近的一個小石凳上,有兩個小孩正在聚精會神地談論著什麼,時而大聲爭論,時而小聲探討。由於好奇心驅使伽菲爾德循聲向兩個小孩走去,想搞清楚兩個小孩到底在幹什麼。只見一個小男孩正俯著身子用樹枝在地上畫著一個直角三角形。於是伽菲爾德便問他們在幹什麼?只見那個小男孩頭也不抬地說:“請問先生,如果直角三角形的兩條直角邊分別為3和4,那麼斜邊長為多少呢?”伽菲爾德答到:“是5呀。”小男孩又問道:“如果兩條直角邊分別為5和7,那麼這個直角三角形的斜邊長又是多少?”伽菲爾德不假思索地回答到:“那斜邊的平方一定等於5的平方加上7的平方。”小男孩又說道:“先生,你能說出其中的道理嗎?”伽菲爾德一時語塞,無法解釋了,心裡很不是滋味。
於是伽菲爾德不再散步,立即回家,潛心探討小男孩給他留下的難題。他經過反覆的思考與演算,終於弄清楚了其中的道理,並給出了簡潔的證明方法。
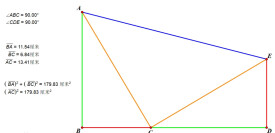
他是這樣分析的,如圖所示:

總統證法
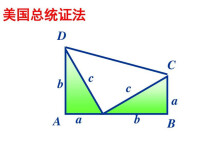
總統證法
1876年4月1日,伽菲爾德在《新英格蘭教育日誌》上發表了他對勾股定理的這一證法。
1881年,伽菲爾德就任美國第二十任總統後來,人們為了紀念他對勾股定理直觀、簡捷、易懂、明了的證明,就把這一證法稱為“總統”證法。
由直角梯形面積公式,得:
直角梯形ABCD面積:S=(a+b)*(a+b)/2
=(a+b)²/2
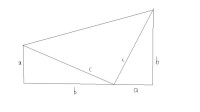
總統證法
CBE面積: =ab/2
CDE面積: =c²/2
∴直角梯形ABCD面積:S= + +
=ab/2+ab/2+c²/2
=(2ab+c²)/2
∴ (a+b)²÷2=(2ab+c²)÷2
∴ (a+b)²=2ab+c²
∴a²+b²+2ab=2ab+c²
∴ a²+b²=c²
∴ a²+b²=c²
他是這樣分析的,如圖1所示:
∵S梯形ABCD=(a+b)
=(a+2ab+b),
又∵S梯形ABCD=S△AED+S△EBC+S△DEC=ab+ba+c=(2ab+c)
∴c=a+b