不可能圖形
二維圖形的別稱
不可能圖形(impossible figure又稱undecidable figure或impossible object)或稱二維圖形,是在現實世界中,不可能客觀存在的事物,只會在二維世界存在的一種圖形。
不可能圖形是由人類的視覺系統瞬間意識地對一個二維圖形的三維投射而形成的光學錯覺,在三維空間中它不可能存在,但研究它將會對人腦圖像形成提供醫學上的幫助。
人們知覺不可能圖形的過程,說明了知覺是人們在感官所獲得的信息的基礎上,對事物主動尋求解釋的一個過程。人們知覺一個事物,總是賦於它一定的意義,並用語言文字把它標誌出來。用語言文字標誌知覺對象也就是知覺者對感覺信息進行組合,尋求最佳解釋的過程,知覺與記憶、思維等活動是密切聯繫著的。人在知覺過程中,能夠識別不可能圖形,正說明過去經驗在知覺中的作用。

合併圖冊
影視
《盜夢空間》中的無盡樓梯
《俠嵐》中三魂之霜的零術空間

不可能圖形
《紀念碑谷》《hocus》
不可能立方體
不可能立方體(Impossible Cube),由M.C.埃舍爾(M. C. Escher)為他的一幅作品《Belvedere》所設計的。不可能立方體簡單描述一下就是在這個立方體中某一條應該靠近觀察者的棱神奇地被一條應該遠離觀察者的棱擋在了更遠處,使人產生錯覺,它在現實世界是不可能客觀存在的。

不可能立方體
彭羅斯三角形(Penrose triangle)第一次是被瑞典藝術家Oscar Reutersvärd創造出來,而後在20世紀50年代被數學家羅傑·彭羅斯(Roger Penrose)所推廣。其特點被以不可能圖形為靈感來創作的藝術家埃舍爾(M. C. Escher)在其作品中很好地體現出來。類似的圖形還有彭羅斯正方形、彭羅斯五邊形等。
彭羅斯階梯(Penrose Stairs),由萊昂內爾·彭羅斯( Lionel Penrose)和他的兒子羅傑·彭羅斯(Roger Penrose)創作。是彭羅斯三角形的一個變式。這是一個由二維圖形的形式表現出來的擁有4個90°拐角的四邊形樓梯。由於它是個從不上升或下降的連續封閉循環圖,所以一個人可以永遠在上面走下去而不會下降。顯然這在三維空間中是不可能的。
潘洛斯階梯,又名潘羅斯階梯、彭羅斯階梯,由英國著名數學物理學家、牛津大學數學系名譽教授潘洛斯(Roger Penrose)提出。潘洛斯階梯是:四條樓梯,四角相連,但是每條樓梯都是向上的,因此可以無限延伸發展,是三維世界里需要在一定角度下才能看到的樓梯。
潘洛斯階梯,曾出現在電影《盜夢空間》(Inception)裡面的清醒夢境(lucid dream)中。Arthur 展示給Ariadne看的奇怪階梯,以及Arthur繞到傭兵背後的樓梯間,這是一座無限循環的階梯。這種不可能出現的物體來自於將三維物體描繪於二維平面時出現的錯視現象。其名稱Penrose來自於英國數學物理學家羅傑·潘洛斯(Roger Penrose),他於1950年代設計了Penrose triangle,潘洛斯寫了幾篇文章討論這些所謂的不可能事件,On the Cohomology of Impossible Figure這篇短文討論了這些對象的群的上同調。Penrose stairs可視為Penrose triangle的一種變形。有名的Penrose stairs出現在荷蘭藝術家M. C. Escher的版畫Ascnding and Descending,以及Waterfall。
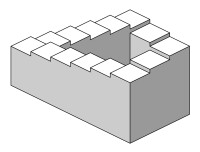
彭羅斯階梯
惡魔的音叉(the devil's fork),它在一端似乎是有3個圓柱的底,在另一端卻莫名其妙地只剩兩個矩形的拐角。相似的作品還有美國藝術家羅傑·霍華德(Roger Hayward)創作的《Undecidable Monument》 。
