調和點列

研究圖形在射影變換下不變性的一個幾何學分支。射影幾何學產生的最初動力，來自為了幫助繪畫而對透視進行的研究。在17世紀，G.德扎格和B.帕斯卡建立了射影幾何學中著名的定理。後來在19世紀，又經過J.V.彭賽列、J.施泰納、K.G.C.von施陶特、A.F.麥比烏斯、A.凱萊等幾何學家的工作，使射影幾何學得到蓬勃的發展，達到鼎盛的時期。

經過有限次兩平面間的中心投影（透視）得到的平面上的一一點變換，稱為平面上的射影變換。

若同一直線上四點滿足

則稱A,B調和分割(harmonic division)線段GH,或調和分割線段AB

為調和點列

G、H與A、B稱為調和共軛(harmonic conjugate).

若△ABC的三條Ceva線共點,

直線交於G,

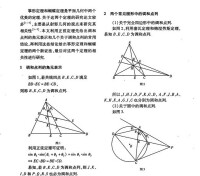
則成調和點列.

對於A,B的內分點C和外分點D滿足C,D調和分割線段AB，M是AB的中點，則有以下結論成立：

1、點A,B調和分割線段CD

2、

3、

4、

設依次在一直線上，若下列命題中任意兩個為真, 則可以推得另外兩個:

1、成調和點列;

2、XB是的內角平分線;

3、

4、XD是的外角平分線

對於直線上的4點把各有向線段的量之間的比值稱為這4點的交比，記為。交比 為－1的4個點組成調和點列。