內切球
內切球
球心到某幾何體各面的距離相等且等於半徑的球是幾何體的內切球。如果一個球與簡單多面體的各面或其延展部分都相切,且此球在多面體的內部,則稱這個球為此多面體的內切球。與圓柱兩底面以及每條母線都相切的球稱為這個圓柱的內切球,此圓柱稱為球的外切圓柱。與圓台的上、下底面以及每條母線都相切的球,稱為圓台的內切球,此圓台稱為球的外切圓台。
內切球球心在幾何體各面上的射影與各面的重心重合,即O‘≡G
半徑的求法:
一般在三稜錐中常用等體積法求半徑,即大三稜錐體積等於以球心為頂點,分割成三稜錐相加,即可求出半徑(高)。
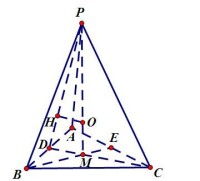
三稜錐
如圖,點M是底邊中線BE、CD的交點,
則圓心O在底面重心M和頂點P的連線上,作OH⊥AD於H,則OH=OM=球半徑R,
為計算表達相對簡便,設底邊=6,側棱=5,
則BD=3,CD=3根號3,PD=4,DM=根號3,PM=根號13,
由△PHO∽△PMD得PO/PD=OH/DM,即(根號13-R)/4=R/根號3,解得R即可。
如果一個球與簡單多面體的各面或其延展部分都相切,且此球在多面體的內部,則稱這個球為此多面體的內切球(inscribed sphere of a polyhedron)。多面體稱為這個球的外切多面體,正多面體的內切球均存在,這裡F為多面體的面數,S為表面積,V為體積。
與圓柱兩底面以及每條母線都相切的球稱為這個圓柱的內切球(inscribed sphere in a circular cylinder),此圓柱稱為球的外切圓柱,等邊圓柱才有內切球,球心在圓柱軸線中點處,內切球半徑與圓柱底面圓半徑相等。
與圓錐的底面和各母線均相切的球,稱為圓錐的內切球(inscribed sphere in a circular cone),此圓錐稱為球的外切圓錐。圓錐的內切球有且僅有一個,球心在圓錐的軸線上。
與圓台的上、下底面以及每條母線都相切的球,稱為圓台的內切球(inscribed sphere in a frustum of a circular cone),此圓台稱為球的外切圓台,當且僅當母線長與上、下兩底面圓半徑之和相等時,圓台才有內切球。
