屈光度

光線由一種物體射入到另一種光密度不同的物質時，其光線的傳播方向產生偏折，這種現象稱為屈光現 象，表示這種屈光現象大小（屈光力）的單位是屈光度（縮寫為“D”）。1D屈光力相當於可將平行光線聚焦在1米焦距上。

眼睛折射光線的作用叫屈光，用光焦度來表示屈光的能力，叫做屈光度。眼睛不使用調節時的屈光狀態，稱為靜態屈光，標準眼靜態屈光的光焦度+58.64D。人眼在使用調節時的屈光狀態，稱為動態屈光，其光焦度強於靜態屈光的光焦度。由於眼睛屈光度不正確，造成不能準確在視網膜成像，就是視力缺陷，一般情況需要佩帶眼鏡，通過鏡片補充和矯正眼睛本身的屈光度，達到視網膜正確成像的目的！

屈光度，或稱 焦度，英語用“Dioptre”表示，是量度透鏡屈光能力的單位。

焦距f的長短標誌著折光能力的大小，焦距越短，其折光能力就越大，近視的原因就是眼睛折光能力太大，遠視的人則折光能力太弱。

焦距的倒數叫做透鏡焦度，或屈光度，用φ表示。如果焦距是10cm，那麼φ=10D。

凸透鏡（如：遠視鏡片）的度數是正數(+)，凹透鏡（如：近視鏡片）的度數是負數(-)。

一個+3屈光度的透鏡，會把平行的光線聚焦在鏡片的1/3米外。

屈光度的單位簡寫是D，國際單位制的單位是 m的-1次方。

一般眼鏡常使用度數來表示屈光度，以屈光度 D 的數值乘以 100 就是度數[1] ，例如 -1.0D 等於近視眼鏡（凹透鏡）的 100度。

主要方法有以下幾種：

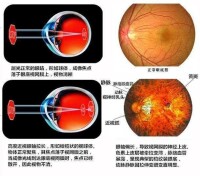
這是一種客觀檢查法。檢查者手持視網膜鏡（中央有孔的小圓反光鏡），離開眼球1米遠，將光線反射到眼球里。光線通過屈光間質到達視網膜，視網膜將光線原路反射出眼球。檢查者通過視網膜鏡中央的小圓孔，可以看到反射回來的光線。由於屈光間質的屈光能力不同，反射光的影像表現不同。影像與視網膜鏡的移動方向一致，稱為順動，反之稱為逆動。遠視眼反射光的影像順動，近視眼反射光的影像逆動。檢查者為了使影像不動，需要不斷在受檢者的眼前加不同的眼鏡片，加到影像靜止為止，說明鏡片已經中和了眼球的屈光不正。換句話說，鏡片的屈光度就是眼球屈光不正的度數。

用自動檢查儀代替檢查者手裡拿的視網膜鏡和各種鏡片。

屈光力越強，焦距越短。2D屈光力的透鏡焦距為1/2m或50cm。如果想知道透鏡的焦距，用100cm，也就是1.00m除以屈光力，結果即為焦距。例如，5D屈光力的焦距為20cm。（100cm除以5D=20cm。）凸透鏡的屈光力以“+”號表示，凹透鏡的屈光力以“—”表示。 1 屈光度或 1D 等於常說的 100 度。

眼鏡的度數=屈光度數×100

在一些光學儀器上比如相機、望遠鏡、顯微鏡等器材上，都考慮到了使用者在不方便佩帶眼鏡觀看時各人

眼睛的視力差異，所以都具有屈光度調節裝置。因此，“屈光度”這個概念是眼鏡的，如200度的近視鏡屈光度為-2D，150度的老花鏡的屈光度為+1.5D。KWP海岸線網路安全資訊站一些高檔相機為了方便一些輕微近視或老花的人群不戴眼鏡可以直接觀看取景器內的效果增加了屈光度調節裝置。屈光度調節裝置其實就是在相機取景目鏡處加一組鏡片，通過旋鈕等調整鏡片位置關係，使其達到一定範圍內的連續屈光度轉換。範圍一般在-3D到+2D之間。由於屈光度調節範圍是有限的，超過這個範圍的中度近視等用戶可以另外選購專用的目鏡調節鏡。專為近視用戶開發的目鏡調節鏡，屈光度分別為-1、-2、-3、-4等；專為遠視用戶開發的目鏡調節鏡，屈光度分別為+0.5、+1、+1.5、+2、+3等。用戶可根據自己的視力情況，選擇合適的目鏡校正鏡加裝在目鏡內，可以裸視進行拍攝。屈光度調節功能不僅在單反相機，並增加部分成本等原因，對於最重視小巧便攜的卡片式數碼相機一般都沒有。屈光度可調眼鏡根據現有通用矯正視力缺陷（近、遠視眼）眼鏡的鏡片形狀固定，屈光度不能調節的缺點，本實用新型將鏡片分為鏡片和透鏡兩部分；透鏡又由鍋底形裡層、外層和液層三層構成。鍋底形裡層的周邊，有一向外轉折且與外層相連的透鏡邊，形成周邊封閉的層狀液體容納空間。鏡片外側的鏡片邊上開有通液孔道，其一端開口於液層，一端與設置在鏡片外側的鏡片邊內的液壓調節裝置相連。當啟動液壓調節裝置，使液層的液體壓力漸漸加大時，則凹透鏡的屈光度由大漸小，而凸透鏡的屈光度則由小漸大；反之，凹透鏡的屈光度由小漸大，而凸透鏡的屈光度則由大漸小，由此實現眼鏡屈光度的自由調節。?

對於同種材料製成的凸透鏡，其凸度越大，屈光度數越大，反之越小。換言之，對同一隻眼球而言，近視度

數越高，眼球越突出，需戴近視鏡度數越高。

眼球的屈光系統是個可調的“凸透鏡”，因而形態可變，當眼前放上凹透鏡時，眼球仍具有自我調節功能，眼睛能看清不同距離的目標和近視或老視患者戴鏡能適應本身就說明了這一點。

由於普通眼鏡與眼球相分離，形象直觀，容易計算。本節探討的重點是眼鏡對眼球屈光的影響，對有關眼鏡的論述，都是針對普通眼鏡。戴角膜接觸鏡與普通眼鏡在屈光方面具有相同的效果，其原理和技術在眼鏡行業已經很成熟，因此不再論述。

在屈光學中，只有在某些特殊情況下，屈光度數為P1、P2兩透鏡組合產生的屈光效果才是屈光度為P1+P2的透鏡。在眼球與透鏡組成的光路中，在效果上或定性的計算中，也可以有P1+P2這種情況，這並非透鏡組合后的實際屈光效果，而是一種簡化和近似，因為眼睛具有自我改變屈光度的能力。雖然較難用實驗驗證，但從眼球的調節效果看，它應當具有抵消鏡片屈光度的作用，而該公式卻具有簡化計算的作用。對於眼球和透鏡所組成的系統來說，至多是兩個透鏡組成的屈光系統，因此可以利用屈光學理論進行計算。當戴上透鏡時，因眼球特殊的調節作用，將透鏡的屈光度和眼球調節適應后的屈光度相加減，也可得到近似值，雖然與準確地測量眼球的屈光力尚有一段距離，但在效果上卻接近。在該論證中，儘管從理論上進行了推導，但實驗和測量都非常困難，就象配製近視鏡需要試戴一樣，在用來指導配鏡的過程中還要進行試驗。

從眼球的屈光特點看，有人測得眼球的靜屈光力為+58.6D,這雖然是一特例，但也基本反映出眼球具有很強

的屈光力，其調節相對較小，正常眼為0——10D左右，近視眼為n——10D(n指眼球的近視屈光度數)左右，而它又固定在眼眶內，因此對某一個人來說，可以認為眼球的屈光系統——“透鏡”的中心到視網膜的距離不變，在以後的計算中，可認為像距為常數K，對於眼球的屈光來說，如果能在視網膜上成清晰的像，該屈光系統仍滿足透鏡成像公式

1/u+1/k=P

其中K是常數，P為眼球的屈光度數，是變數，意思是不同的人看不同距離的目標和不同的人眼球的屈光度數不同，U指目標到眼球的距離。該公式成立的條件是：某一時刻，眼睛看某一距離的目標，且目標在眼睛的近、遠點之間。從公式看，正視眼看無窮遠處時1/u=0，上式可化為P=1/K，可令1/k=P0,即P0為眼球的靜屈光度。當看距眼球為L的目標時，“透鏡”成像公式變為1/L+1/K=1/L+P0,1/L為眼球增加的屈光度數，1/L+P0即為眼球看距離為L的目標時的屈光度。

對於戴鏡者來說，在一般情況下，眼球到眼鏡中心的距離約為1.2——2.4CM,以下用h表示，但對於某人某一時刻的值是確定的，設屈光度為P'的透鏡的焦距為F，當看距離為L的目標時，鏡片成像公式如下:

1/L+1/V=P'==>1/V=P'-1/L①

此時透鏡所成像到眼球這一“透鏡”的距離為|V|+h,眼球的屈光情況滿足公式:1/(|V|+h)+1/K=P②

從公式看，如果|V|比h大得多，根據①公式，②式可近似簡化為:

1/|V|+1/K=D=|D'-1/L|+1/K③

由於眼睛透過透鏡看到的是虛像，V<0,則1/|V|+1/K=1/L+1/K-D'=D1+D0-D'

從該公式看，|V|的大小取決於物距L和透鏡的焦距，考慮到實際情況，近視眼鏡的屈光度大多數大於-6D，學生看書、寫字的距離大多大於0.25M,而且根據透鏡成像公式可知，凹透鏡屈光度數P'(注D'<0,下同)越小，V|越小，物距越小，|V|越小，如當D'=-5，U=0.25時，V|=0.111M，仍比0.02M大很多。所以作為理論

計算，在看距離不太近、鏡片度數不太高的目標時，可忽略h，這樣可簡化計算，有利於定性分析。換言之，對於薄透鏡來說，如果忽略眼球到鏡片的距離，可以認為因戴近視眼鏡致使眼球調節增加的調節度數等於透鏡的屈光度數。在眼球與眼鏡組成的光學系統中，各部分所產生的屈光度數可近似相加減，這種分析可使計算簡化，使問題變得容易。在以後的論述中，我們將利用這一結果進行定性分析和近似計算。

誤差分析。如果以公式為標準，那麼產生誤差的原因是多方面的，現對此分析。

(1)因為眼球的調節與形變同時進行，有調節就有形變，有形變就有眼球前後徑的變化，還由於晶狀體和角膜本身形變而導致的角膜、房水、晶狀體所組成的“凸透鏡”光心的變化。雖然近視或老視本身並不能說明其前後徑的變化(一說，近視眼是眼球成像在視網膜前方，但近調節的過強或睫狀肌不能放鬆都可實現這一點，不能充分說明眼球前後徑變長)，但更不能說明其不變性。這些因素的存在決定了公式中K只是一個近似，而且近調節幅度越大，K值變化越大，這是產生誤差的一個原因。但考慮到在眼球調節中，晶狀體的屈光度調節和眼球的屈光度(約60屈光度)相差很遠，而眼球調節幅度一般少於10個屈光度，相對較小，角膜屈光度變化更小，因此，可認為“透鏡”光心到視網膜的距離幾乎不變。

(2)因每個人的眼球前後徑不等，對不同的人而言，K並非常數，很難準確測量，但具體到某一個人的某一階段而言，眼球前後徑不變，可認為K是常數。

(3)對不同的人而言，眼鏡片到“凸透鏡”光學中心的距離是一較難測量的變數，這也影響到計算的準確性。由計算可知，h增大時，誤差增大，反之越小。

在眼前放置透鏡時，與正常眼相比，如果眼睛仍然能看清目標，從眼球的調節效果看，眼鏡首先抵消眼球調節的不足，因此在以後的計算中，只要在眼球正常的調節範圍內，用於抵消透鏡的效果在理論上能夠成立，我們無須注意眼球實際屈光度的變化。對眼球來說，不管戴多少屈光度的眼鏡，要看清前面的目標，必須低消眼鏡的作用而增加屈光度調節。

由於配鏡誤差、適應等原因，即使把各種因素都考慮進去，理論對於實踐也只是一種近似，眼球調節幅度較大時，這種簡單化、理想化的理論會因自身形變而使誤差增大。再者，鏡片到眼球光學中心的距離隨不同的人而不同，這又無法用物理公式表示，在具體配製時要具體問題具體分析。

對於眼球和鏡片所組成的屈光系統來說，鏡片度數是確定的，而眼球的屈光度數卻是個變數，因此，把眼球看成是一個可調凸透鏡的意思是：眼睛透過眼鏡能看清某一目標時，眼球的屈光度數確定，因而完全可以利用屈光學理論進行計算，但眼球看目標的距離發生變化時，其屈光度數也隨之變化。

對眼球與眼鏡組成的屈光系統而言，只有兩個“透鏡”組成，可看成一個等效的透鏡組，透鏡的度數可相加減，比如一個+5D的透鏡，可看成是一個(+2D)+(+3D)的透鏡組，雖然在多數情況下並不成立，但在理論為我們解決問題提供了方便。