圖像金字塔
圖像金字塔
圖像金字塔是圖像多尺度表達的一種,是一種以多解析度來解釋圖像的有效但概念簡單的結構。一幅圖像的金字塔是一系列以金字塔形狀排列的解析度逐步降低,且來源於同一張原始圖的圖像集合。其通過梯次向下採樣獲得,直到達到某個終止條件才停止採樣。我們將一層一層的圖像比喻成金字塔,層級越高,則圖像越小,解析度越低。
如上述定義所說,一幅圖像的金字塔是一系列以金字塔形狀排列的解析度逐步降低的圖像集合。金字塔的底部是待處理圖像的高解析度表示,而頂部是低解析度的近似。當向金字塔的上層移動時,尺寸和解析度就降低。因為基礎級J的尺寸是2^J*2^J或N*N(J=log2N),所以中間級j的尺寸是2^j*2^j,其中0<=j<=J。完整的金字塔由J+1個解析度級組成,由2^J*2^J到2^0*2^0,但大部分金字塔只有P+1級,其中j=J-P,…,J-2,J-1,J,且1<=P<=J。也就是說通常限制它們只使用P級來減少原始圖像近似值的尺寸。例如,一幅512*512圖像的1*1或單像素近似值將非常小。右圖顯示了一個建立圖像金字塔的簡單系統。j-1級的近似輸出用來建立近似值金字塔,包括原始圖像的一個或多個近似值。作為金字塔的原始圖像和它的P級減少的解析度近似都能直接獲取並調整。j級的預測殘差輸出用於建立預測殘差金字塔。這些金字塔包括了原始圖像的J-P級低解析度的近似信息,以及建立P級較高解析度的近似信息。j級的信息在相應近似金字塔的j級近似與基於j-1級預測殘差得到的近似估計之間是不同的。對這些差異進行編碼(用於存儲或傳輸)將比對近似值進行編碼有效得多。
如框圖所表明的,近似值和預測殘差金字塔都是以一種迭代的方式進行計算的。通過執行P次框圖中的操作建立P+1級金字塔。第一次迭代和傳遞時,j=J,並且2^J*2^J的原始圖像作為J級的輸入圖像,從而產生J-1級近似值和J級預測殘差。對於j=J-1,J-2,…,J-P+1(按這一順序)的傳遞,前面迭代的j-1級近似值輸出將作為輸入。每次傳遞由3個連續步驟組成:
1.計算輸入圖像減少的解析度的近似值。這可以通過對輸入進行濾波並以2為步長進行抽樣(即子抽樣)。可以採用的濾波操作有很多,如鄰域平均(可生成平均值金字塔),高斯低通濾波器(可生成高斯金字塔),或者不進行濾波,生成子抽樣金字塔。生成近似值的質量是所選濾波器的函數。沒有濾波器,在金字塔的上一層中的混淆變得很顯著,子抽樣點對所選取的區域沒有很好的代表性。
2.對上一步的輸出進行內插(因子仍為2)並進行過濾。這將生成與輸入等解析度的預測圖像。由於在步驟1的輸出像素之間進行插值運算,所以插入濾波器決定了預測值與步驟1的輸入之間的近似程度。如果插入濾波器被忽略了,則預測值將是步驟1輸出的內插形式,複製像素的塊效應將變得很明顯。
3.計算步驟2的預測值和步驟1的輸入之間的差異。以j級預測殘差進行標識的這個差異將用於原始圖像的重建。在沒有量化差異的情況下,預測殘差金字塔可以用於生成相應的近似金字塔(包括原始圖像),而沒有誤差。
執行上述過程P次將產生密切相關的P+1級近似值和預測殘差金字塔。j-1級近似值的輸出用於提供近似值金字塔,而j級預測殘差的輸出放在預測殘差金字塔中。如果不需要預測殘差金字塔,則步驟2和3、內插器、插入濾波器以及圖中的加法器都可以省略。
金字塔的重要應用-圖像融合
在圖像處理學科里,圖像金字塔被廣泛的用於圖像融合,圖像金字塔融合原理可用下圖直白的表示:
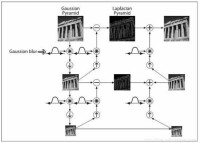
圖像金字塔
