三階幻方
三行三列的矩陣
三階幻方是最簡單的幻方,又叫九宮格,是由1,2,3,4,5,6,7,8,9九個數字組成的一個三行三列的矩陣(如右圖示),其對角線、橫行、縱向的和都為15,稱這個最簡單的幻方的幻和為15。中心數為5。
相傳,大禹治水時,洛水中出現了一個“神龜”背上有美妙的圖案,史稱“洛書”,用現在的數字翻譯出來,就是三級幻方。
2500年前,孔子在他研究《易經》的著作《系詞上傳》中記載了:“河出圖,洛出書,聖人則之。”最早將數字與洛書相連的記載是2300年前的《莊子·天運》,它認為:“天有六極五常,帝王順之則治,逆之則凶。九洛之事,治成德備,監照下土,天下戴之,此謂上皇。”明代數學家程大位在《演演算法統宗》中也曾發出“數何肇?其肇自圖、書乎?伏羲得之以畫卦,大禹得之以序疇,列聖得之以開物”的感嘆,大意是說,數起源於遠古時代黃河出現的河圖與洛水出現的洛書,伏羲依靠河圖畫出八卦,大禹按照洛書劃分九州,並制定治理天下的九類大法,聖人們根據它們演繹出各種治國安邦的良策,對人類社會與自然界的認識也得到步步深化。大禹從洛書中數的相互制約,均衡統一得到啟發而制定國家的法律體系,使得天下一統,歸於大治,這是借鑒思維的開端。這種活化思維的方式已成為科學靈感的來源之一。從洛書發端的幻方在數千年後的今天更加生機盎然,被稱為具有永恆魅力的數學問題。十三世紀,中國南宋數學家楊輝在世界上首先開展了對幻方的系統研究,歐洲十四世紀也開始了這方面的工作。著名數學家費爾瑪、歐拉都進行過幻方研究,如今,幻方仍然是組合數學的研究課題之一,經過一代代數學家與數學愛好者的共同努力,幻方與它的變體所蘊含的各種神奇的科學性質正逐步得到揭示。目前,它已在組合分析、實驗設計、圖論、數論、群、對策論、紡織、工藝美術、程序設計、人工智慧等領域得到廣泛應用。1977年,4階幻方還作為人類的特殊語言被美國旅行者1號、2號飛船攜入太空,向廣袤的宇宙中可能存在的外星人傳達人類的文明信息與美好祝願!
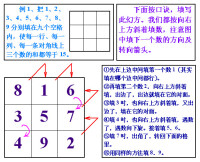
三階幻方
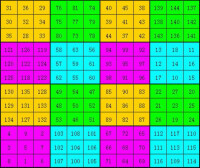
由三階基本幻方各數減1生成的新幻方
由1、2、3、……等連續自然數生成的幻方為 基本幻方,在此基礎上各數再加或減一個相同的數,可組成由零或負數組成的新幻方,新
如上圖基本幻方中各數減1生成的新幻方,幻和為12,如下圖示:
拆填方式
想:1+9=10,2+8=10,3+7=10,4+6=10。這每對數的和再加上5都等於15,可確定中心格應填5,這四組數應分別填在橫、豎和對角線的位置上。先填四個角,若填兩對奇數,那麼因三個奇數的和才可能得奇數,四邊上的格里已不可再填奇數,不行。若四個角分別填一對偶數,一對奇數,也行不通。因此,判定四個角上必須填兩對偶數。對角線上的數填好后,其餘格里再填奇數就很容易了。
古代方式
南宋數學家楊輝概括的構造方法為:
“九子斜排。上下對易,
左右相更。四維突出。”
中國古代九宮格的填法口訣是:
九宮之義,法以靈龜,
二四為肩,六八為足,
左七右三,戴九履一,
五居中央。
也有把這兩者綜合起來說的:
九子斜排,上下對易,
左右相更,四維挺出,
戴九履一,左七右三,
二四為肩,六八為足
即:
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
或
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
奇階幻方通用構造法
口訣:
1 居上行正中央,
依次斜填切莫忘,
上出框界往下寫,
右出框時左邊放,
重複便在下格填,
出角重複一個樣。
解釋:
1)在第一行居中的方格內放1,依次向右上方填入2、3、4…;
2)如果這個數所要放的格已經超出了頂行那麼就把它放在底行,仍然要放在右一列;
3)如果這個數所要放的格已經超出了最右列那麼就把它放在最左列,仍然要放在上一行;
4)如果右上方已有數字和出了對角線,則向下移一格繼續填寫。
5)也可將所填數在幻方中所對應的數填在幻方中對應的位置。
例如:1為第一行中間數,則將對應的9填在最後一行的中間。2以次類推。
按照這種方式,做鏡像或旋轉對稱,可得到實際相同的其他填法:
只要將1放於四個變格的正中,向幻方外側依次斜填其餘數字;若出邊,將數字調到另一側;若目標格已有數字或出角,回一步填寫數字,再繼續按一開始的相同方向依次斜填其餘數字。
用1~9填出的三階基本幻方的所有情況都是相互鏡像或旋轉的。
是本質相同的不同表現:
第一種:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
第二種:
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
第三種:
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
第四種:
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
第五種:
| 6 | 7 | 2 |
| 1 | 5 | 9 |
| 8 | 3 | 4 |
第六種:
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
第七種:
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
第八種:
| 4 | 3 | 8 |
| 9 | 5 | 1 |
| 2 | 7 | 6 |
任意等差數列
任意等差數列都可以由1~9的每個數乘以X,再加Y,得到。
因此按照原先的從小到大的順序排列,幻方仍然成立。
例如要用6、9、12、15、18、21、24、27、30構成幻方:
把1-9構成的3階幻方的每個數乘以3,再加3:
| 27 | 6 | 21 |
| 12 | 18 | 24 |
| 15 | 30 | 9 |
幻和值=54
等差的三組等差
3個一組的數,組與組等差,每組數與數等差,這樣的數能構成3階幻方。
同樣按照基本幻方的大小排列他們的順序即可
例如以下3組9個數:
【2、4、6】、【13、15、17】、【24、26、28】構成幻方,
| 26 | 2 | 17 |
| 6 | 15 | 24 |
| 13 | 28 | 4 |
幻和值=45。
以下規律對所有三階幻方均成立:
幻和=3×中心數
證明:
通過中心數有4條線。將這4條線全部加起來,可以得到:
幻和×4=全體數的和+中心數×3
而我們知道三階幻方中,全體數的和=3×幻和(三行或三列)
因此有:
幻和×4=幻和×3+中心數×3
化簡得到:
幻和=3×中心數
過中心的線上的三個數,依次成等差數列。或者說,關於中心位置對稱的兩數,平均數是中心數。
證明:
過中心線的三個數之和為幻和。性質1已經說明,幻和=3×中心數。
因此中心數是這三個數的平均數。
從這之中去掉中心數不改變平均數。
因此中心數是關於中心位置對稱的兩數。
也就是一個數比中心數多多少,另一個數就比中心數少多少。即他們成等差數列
2倍角格的數=不相鄰的2個邊格數之和。2a=b+c
如:基本幻方中:2*8=9+7,2*4=1+7,2*6=3+9,2*2=1+3
| a | ||
| c | ||
| b |
證明:
過a有3條線。計算這三條線的和:
幻和×3=全體數的和+2×a-b-c
而
全體數的和=幻和×3
因此
2×a-b-c=0
2×a=b+c
