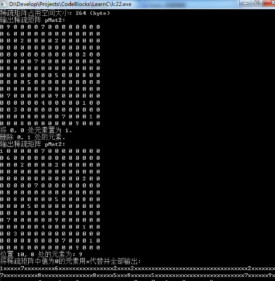
稀疏矩陣
元素大部分為零的矩陣
稀疏矩徠陣(sparse matrix)是其元素大部分為零的矩陣。
稀疏矩陣
非零元素佔全部元素的百分比很小(例如5%以下)的矩陣。有的矩陣非零元素佔全部元素的百分比較大(例如近50%),但它們的分佈很有規律,利用這一特點可以避免存放零元素或避免對這些零元素進行運算,這種矩陣仍可稱為稀疏矩陣。
給定一個N×M的稀疏矩陣A,其第n行的行帶寬定義為:
整個矩陣的帶寬定義為:

稀疏矩陣
稀徠疏矩陣的計算速度更快,因為MATLAB只對非零元素進行操作,這是稀疏矩陣的一個突出的優點。假設矩陣A,B中的矩陣一樣。計算2*A需要一百萬次的浮點運算,而計算2*B只需要2000次浮點運算。因為MATLAB不能自動創建稀疏矩陣,所以要用特殊的命令來得到稀疏矩陣.
對於一個用二維數組存儲的稀疏矩陣Amn,如果假設存儲每個數組元素需要L個位元組,那麼存儲整個矩陣需要m*n*L個位元組。但是,這些存儲空間的大部分存放的是0元素,從而造成大量的空間浪費。為了節省存儲空間,可以只存儲其中的非0元素.
對於矩陣Amn的每個元素aij,知道其行號i和列號j就可以確定其位置。因此對於稀疏矩陣可以用一個結點來存儲一個非0元素。該結點可以定義如下:[i,j,aij] 該結點由3個域組成,i:行號,j:列號;aij元素值。這樣的結點被稱為三元組結點。矩陣的每一個元素Qij,由一個三元組結點(i,j,aij)唯一確定.
例如稀疏矩陣A:
50000
100200
0000
-300-605
其對應的三元組表為:
0050
1010
1220
30-30
32-60
335
解線性方程組的直接法的稀疏矩陣技術,根據不同領域中不同問題的特點,有各種不同稀疏解法。最常用的方法有稀疏去零消元法、等帶或變帶寬消元法、波陣法、子結構法、撕裂和修改技術等,它們都只不過是消元法或三角分解法在各種具體場合下的運用。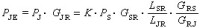

稀疏矩陣

稀疏矩陣
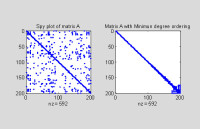
各種消元法方案中的關鍵問題都是方程式和未知數的排序問題。確切地說,就是在用某種直接法解稀疏線性方程組時,對方程式和未知數進行適當排序,使得在滿足一定的穩定性要求的前提下,解方程組所需的運算量和存貯量最少。一般說來,這等價於使新產生的非零元(“添補數”)最少。例如,對矩陣作一步消元法,將A變成,右下角矩陣是滿的,A的零元所在位置上產生了許多非零元,破壞了稀疏性,這就要增加許多存貯量和運算量;如果將矩陣A的第一行與最後一行,第一列與最後一列交換,這相當於重新排列方程式和未知數的次序,得矩陣,對Ã作消元法時,不會有新的非零元產生,存貯量和運算量大大減少。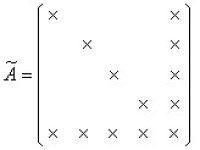

稀疏矩陣
與常用的演演算法相對應,排序問題可分為以下三類:①預先把矩陣排列成帶型或變帶寬型,並使帶寬或剖面儘可能小;②預先把矩陣排列成塊三角矩陣或其他特殊分塊矩陣;③在稀疏消元法的消元過程中,根據產生添補數最少的原則來確定選主元的次序(這也是一種排序)。對一般矩陣,排序問題是一個非常困難的問題,因為對一個給定的矩陣來說,所有可能的次序總數是一個巨大的數字,可以給出的排序演演算法只是按某一特殊準則來確定“最佳次序”的。討論中常用圖論作為工具。
稀疏矩陣的存貯並沒有一種最好的方式,在各種具體情況下,最好的方式與要存貯矩陣的結構及用途有關一種好的標準是矩陣的元素容易查找而且存貯量少。存貯方式基本上採用壓縮形式,使矩陣中大量的零元素不參加運算,以減少機器的運行時間,並可提高機器處理高階矩陣問題的能力。
對於帶型矩陣,只存貯帶內或剖面內的元素。如對矩陣
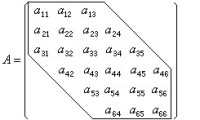
稀疏矩陣
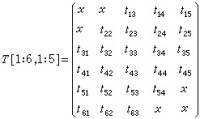
稀疏矩陣
對於對稱帶型陣
稀疏矩陣
可用變帶寬存貯法。它需要兩個數組:①存放剖面內的元素的一維數組S【1:11】={b11,b21,b22,b31,0,b33,b44,b53,0,b55,b66};②對角元數組D【1:6】={1,3,6,7,10,11},在它的第i個位置上存放對角元bii在數組S中的序號。這樣,矩陣的元素bij可通過D,i,j在S中找到。對應關係為
稀疏矩陣
對於元素隨機分佈的稀疏矩陣,只存貯矩陣的非零元素和必要的檢索信息。如對

稀疏矩陣
此外,還有連接表存貯法和超矩陣存貯法等。
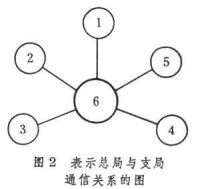
稀疏矩陣
矩陣微積分迭代存貯