帕普斯定理
帕普斯定理
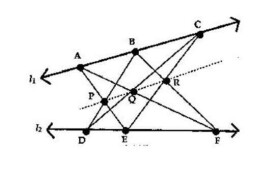
帕普斯(Pappus)定理,指的是直線l1上依次有點A,B,C,直線l2上依次有點D,E,F,設AE,BD交於P,AF,DC交於Q,BF,EC交於R,則P,Q,R共線。
設U,V,W,X,Y和Z為平面上六條直線。如果: (1)U與V的交點,X與W的交點,Y與Z的交點共線,且(2)U與Z的交點,X與V的交點,Y與W的交點共線,則(3)U與W的交點,X與Z的交點,Y與V的交點共線。這個定理叫做帕普斯定理。

證明方法1
(證明過程見右圖)
證明方法2
利用布列安桑定理及其逆定理證明:
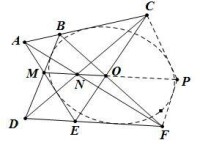
證明方法2
延長MO至P,由布列安桑逆定理知六邊形PCBMEF內切圓錐曲線,由凹六邊形AMDFPC及其內切圓錐曲線的布列安桑定理知對角線,則M、N、O共線,帕普斯定理得證。
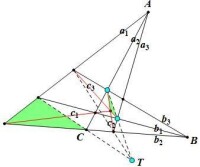
帕普斯定理
該對偶命題仍然可以利用帕普斯定理(幾何變換形態)及笛沙格定理(逆)證明
定理2
由射影幾何中的對偶原理(此處體現為點線互換)可知,它與帕普斯(Pappus)定理是等價的。
該對偶命題是布利安桑定理的特例。
明顯的,當二次曲線上的帕斯卡定理中二次曲線退化為兩條相交直線(在射影平面中,我們認為平行直線相交於無窮遠點),即為帕普斯(Pappus)定理。