笛沙格定理
笛沙格定理
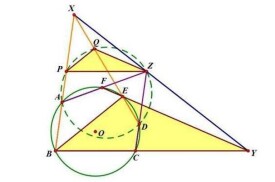
笛沙格定理,數學幾何定理,即同調三角形定理。平面上有兩個三角形△ABC、△DEF,設它們的對應頂點(A和D、B和E、C和F)的連線交於一點,這時如果對應邊或其延長線相交,則這三個交點共線。其逆定理也成立。
笛沙格定理本身為自對偶定理。
笛沙格定理
此時,這兩個三角形被稱為“透視的”。
梅涅勞斯定理證法
(見右圖)
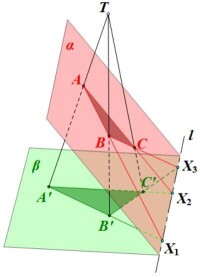
立體(射影)證法
平面α∩平面β=直線l,異於二平面外一點T引三條直線分別交平面α、平面β於A、A',B、B',C、C',設TA'與TB'構成的平面為π,平面α∩平面π=AB,平面β∩平面π=A'B',則平面α∩平面β∩平面π=X=AB∩A'B'且X∈l,同理X∈l,X∈l,則平面笛沙格定理即直觀所示,得證。
P.S:其逆定理也成立
笛沙格對合定理Desargues' Involution Theorem
一條直線與一個完全四點形的三雙對邊的交點與外接於該四點形的圓錐曲線構成一個對合的四個點偶,一個點與一個完全四線形的三雙對頂點的連線和從該點向內切於該四線形的圓錐曲線所引的切線構成一個對合的四個射線偶合。
一個完全四點形(四線形)實際上含有四點(線)1,2,3,4和它們的六條連線交點23,14,31,24,12,34;其中23與14、31與24、12與34稱為對邊(對頂點)。
笛沙格研究了兩空間笛沙格構圖成透射時的透射比問題,它是繼兩空間笛沙格構圖成透射的條件及透射定位參數的確定問題之後,針對透射參數的研究。在過去研究工作基礎上,運用幾何分析方法,得到了求兩空間笛沙格構圖成透射時的透射比的計算公式,給出精確計算結果。將兩空間笛沙格構圖成透射的參數補齊,得到的透射比公式中含有耦合配位三角形中的幾何關係,使透射比的表達更加簡明。
平面笛沙格定理
如圖,從O引射線A1A2、B1B2、C1C2。則B1A1與B2A2交於X,B1C1與B2C2交於Y,A1C1與A2C2交於Z,則X、Y、Z共線。可以用梅涅勞斯定理證明。
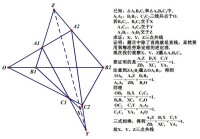
笛沙格定理
笛沙格定理在空間里也是成立的,證明也是非常簡單的。
笛沙格定理