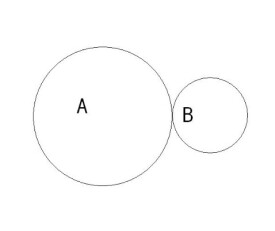
兩圓相切

兩圓間的位置關係

兩圓相切(contact of two circles)兩圓間的一種位置關係.指兩圓只有惟一的公共點.惟一的公共點稱為切點。與一般的平面二次曲線相比，由於圓所具有的旋轉對稱性，使得關於圓的相切有許多優美和深刻的結果。

目錄

1基本介紹 2釋義詳解

基本介紹

相切兩圓分兩圓外切和兩圓內切兩種情況.兩圓外切是指除它們的公共點外，每個圓上的點都在另一個圓的外部(如圖1左圖).兩圓外切的充分必要條件是圓心距等於兩圓半徑的和，即.兩圓內切是指除它們的公共點外，一個圓上的點都在另一個圓的內部(如圖1右圖).兩圓內切的充分必要條件是圓心距等於兩圓半徑的差的絕對值，即，兩圓重合即，可看做兩圓內切的特例。兩圓相切時，連心線必過切點。

釋義詳解

tagency of two circles

兩圓相切有兩種情況:

1.兩圓外切

兩圓外切時兩圓的連心線垂直於兩圓的內公切線

(設兩個圓的半徑為R和r,當時，兩圓連心線與外公切線平行)

2.兩圓內切

兩圓內切時一圓在另一圓內且兩圓的連心線垂直於兩圓的公共切線

附加兩個定理:

定理1：相切兩圓的連心線（經過兩個圓心的直線）必經過切點

定理2：設兩個圓的半徑為R和r，圓心距為d，則

（1）兩圓外切

（2）兩圓內切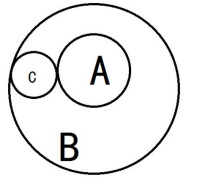

兩圓相切

兩圓相切

目錄