麥克勞林公式
數學學科的專業術語
麥克勞林公式是一個數學學科的專業術語,指泰勒公式(在x。=0下)的一種特殊形式,麥克勞林公式是泰勒公式在0點展開的特例。
麥克勞林公式是18世紀英國最具有影響的數學家之一麥克勞林(Colin Maclaurin)發現提出的,麥克勞林得到數學分析中著名的Maclaurin級數展開式,並用待定係數法給予了證明,因此公示以麥克勞林命名。使用麥克勞林公式時,是不可能將被展開的函數完全展開的,所以只能展開一部分,用一個近似公式,而由這個式子計算出的結果也是近似指。
麥克勞林公式是泰勒公式在下的一種特殊形式。
若函數在開區間有直到n+1階的導數,則當函數在此區間內時,可以展開為一個關於多項式和一個余項的和:
其中是公式的余項,可以是如下:
| 皮亞諾(Peano)余項 | |
| 爾希-羅什(Schlomilch-Roche)余項 | 是的階導數, |
| 拉格朗日(Lagrange)余項 | 是的階導數, |
| 柯西(Cauchy)余項 | 是的階導數, |
| 積分余項 | 是的階導數 |
簡介

麥克勞林
1719年Maclaurin在訪問倫敦時見到了Newton,從此便成為了Newton的門生。他在1742年撰寫的名著《流數論》是最早為Newton流數方法做出了系統邏輯闡述的著作。他以熟練的幾何方法和窮竭法論證了流數學說,還把級數作為求積分的方法,並獨立於Cauchy以幾何形式給出了無窮級數收斂的積分判別法。他得到數學分析中著名的Maclaurin級數展開式,並用待定係數法給予證明。
Maclaurin終生不忘牛頓Newton對他的栽培,死後在他的墓碑上刻有“曾蒙 Newton的推薦”以表達他對Newton的感激之情。成就他在代數學中的主要貢獻是在《代數論》(1748,遺著)中,創立了用行列式的方法求解多個未知數聯立線性方程組。但書中記敘法不太好,後來由另一位數學家Cramer又重新發現了這個法則,所以現在稱為Cramer法則。Maclaurin的其他論述涉及到天文學,地圖測繪學以及保險統計等學科,都取得了很多創造性的成果。
公式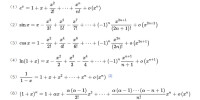
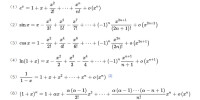
麥克勞林公式
