極大值原理
極大值原理
極大值原理是對分析力學中古典變分法的推廣,能用於處理由於外力源的限制而使系統的輸入(即控制)作用有約束的問題。極大值原理是20世紀50年代中期蘇聯學者Л.С.龐特里亞金提出的,有關這一原理的主要結果及其嚴格的數學證明,都發表在後來出版的《最優過程的數學理論》一書中。
最優控制理論中用以確定使受控系統或運動過程的給定性能指標取極大或極小值的最優控制的主要方法。在工程領域中很大一類最優控制問題都可採用極大值原理所提供的方法和原則來定出最優控制的規律。在理論上,極大值原理還是最優控制理論形成和發展的基礎。
最優控制問題是從大量的工程實際問題(特別是航天和航空技術問題)中提煉出來的一個控制理論問題。最優控制問題有四個要素。
通常採用狀態方程(見狀態空間法)的形式,它是狀態向量x的一階微分方程夶=f(x,u,t),其中u為控制向量,t為時間變數。在最一般的情況下,受控系統是非線性(見非線性控制系統)和時變(見時變系統)的,所以f(x,u,t)為非線性和時變的向量函數。
工程實際因素的限制決定了控制器的允許類型。一個容許控制只能在控制的容許類中選取。用U表示系統的控制的允許類,則在數學上可將容許控制u表示為u∈U。通常U受到封閉性的邊界限制。
在控制作用下系統狀態所要達到的目標區。這個目標區可以是一個給定的點,也可以是一個給定的區域。用tf表示運動過程的末時刻,x(tf)表示末時刻系統的狀態,則目標集常可用向量等式g1(x(tf),tf)=0、向量不等式g2(x(tf),tf)≤0來描述。
式1
反映和評價系統性能優劣的指標。性能指標的形式由實際問題來決定,通常有兩種類型:表示系統在末時刻狀態的性能指標稱為末值型性能指標,記為S(x(tf),tf);用特定函數的積分表示系統運動過程中的性能的指標稱為積分型性能指標,記為式1 其中t0為初始時刻。性能指標的一般形式為 式2 稱為混合型性能指標。性能指標值的大小依賴於控制作用的整體u(·)的選擇,而不是取決於控制u在t時刻的值;因此J【u(·)】是控制函數u(·)的函數(稱為u(·)的泛函)。
最優控制問題可表述為:尋求一個容許控制u(t),以使受控系統從某個給定的初始狀態x(t0)=x0出發,在末時刻tf達到目標集,並且使性能指標泛函J【u(·)】達到極小值或極大值。如果這個問題是有解的,那麼就稱求得的容許控制為最優控制,記為u*(t);而系統狀態方程在u*(t)作用下的解稱為最優軌線,記為x*(t);相應的極小或極大性能指標值J【u*(·)】,稱為最優指標值。在數學上,最優控制問題的實質,是對受約束的泛函J【u(·)】求極值的問題,其中的約束條件為系統的狀態方程、目標集方程和容許控制域。
對於定常系統的最優控制問題的極大值原理可表述如下:如果最優控制問題的數學模型為:受控系統夶=f(x,u),x(t0)=x0,t∈【t0,tf】
目標集g1(x(tf))=0 ,g2(x(tf))≤0
容許控制u∈U
性能指標J【u(·)】=S(x(tf))
末時刻tf自由
則u*(t)為最優控制、x*(t)為最優軌線和tf為最優末時刻的必要條件有五項。
① x*(t)滿足方程(式3)
② λ(t)滿足方程(式4)式中(式5)稱為給定問題的哈密頓函數,λ^T(t)為λ(t)的轉置。λ(t)稱為狀態x(t)的伴隨狀態,而其方程稱為伴隨方程。
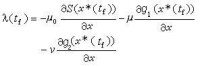
式6
④ u*(t)滿足條件(式7) ⑤ 確定t壚的方程為(式8)極大值原理的名稱就來自於條件④。據此定出最優控制u*(t)的關係式后,最優控制問題的求解就歸結為對運動方程及其初始條件x(t0)和伴隨方程及其末時刻條件λ(tf)聯合求解,這種問題稱為兩點邊值問題。更一般形式的最優控制問題(包括受控過程為時變系統、性能指標為積分型指標或混合型指標、末狀態的約束方程為更複雜的形式等情況)的極大值原理的結果都可由上述基本形式導出。
在一般情況下,由極大值原理定出的最優控制是時間變數t的函數u*(t),稱為程序控制或開環控制。程序控制的主要缺點,是不能消除或抑制由於參數的變動和環境的變化對系統造成的擾動。最優控制的另一類形式是表示為狀態變數x*(t)的函數u*(x*),實質上是一種狀態反饋,稱為綜合控制或閉環控制,其優點是對抑制擾動有利。原則上極大值原理能夠用來確定綜合控制形式的最優控制,但除了一些典型的最優控制問題外,對於一般的情況決定綜合控制往往相當困難。在工程領域中,最為常見的一種綜合控制形式是所謂的砰-砰控制。在這類控制形式中,根據系統的運動狀況,最優控制u*的各個控制變數在整個過程中分段地取為容許控制範圍的正最大值或負最大值。砰-砰控制的原理是把最優控制問題歸結為:將狀態空間劃分為兩個區域,一個區域對應於控制變數取正最大值,另一個區域對應於控制變數取負最大值。這兩個區域的分界面稱為開關面,而決定砰-砰控制的具體形式的關鍵就是決定開關面。砰-砰控制形式的最優控制常用於最速控制系統和最省燃料控制系統。在正常情況下,砰-砰控制的控制變數由正最大值躍變到負最大值的次數是有限的,只有在躍變瞬時控制變數可取值於限制範圍的任何值。但對於某些問題,砰-砰控制中至少存在一個時間區間,其中控制變數可取為限制範圍的任意值,這類問題稱為奇異最優控制問題。對於奇異最優控制問題,僅由極大值原理的條件還不足以確定奇異時間區間內的最優控制u*與最優軌線x*間的關係即綜合控制的形式。
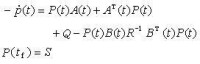
式11
式13
LQ 問題 線性二次型性能指標的最優控制問題。在LQ問題中,受控系統為線性系統,運動方程具有形式夶=A(t)x+B(t)u;性能指標是狀態x和控制u的一個二次型函數的積分,可表示為(式9)其中加權陣S和Q為半正定對稱陣,R為正定對稱陣;控制u的各個控制變數的取值範圍不受限制。根據極大值原理很容易定出LQ問題的最優控制(式10)它是一種線性狀態反饋形式的綜合控制。其中R^-1表示矩陣R的逆,B^T(t)表示矩陣B(t)的轉置,而P(t)為正定對稱矩陣,是如下的矩陣黎卡提微分方程(式11)的解:在工程領域中,很多情況下受控系統是定常系統,即其運動方程為夶=Ax+Bu,且取初時刻t0=0,而末時刻tf=∞,性能指標泛函為(式12)這時只要矩陣對(A,B)為能控(見能控性),矩陣對(A,C)為能觀測(見能觀測性),其中C為由分解Q=CC^T導出的矩陣,那麼最優控制u*=-Kx*具有狀態x*的線性定常反饋的形式,反饋矩陣K=R^-1B^TP,P為如下的矩陣黎卡提代數方程(式13)的解 這類控制問題的優點是反饋矩陣K為常數,可由計算機事先通過計算定出,不必在控制系統中引入計算機進行實時控制。LQ問題在工程上常稱為線性調節器問題。
對於較為複雜的受控系統,即使系統為線性的情況,最優控制問題的求解也常有大量的計算。採用次優控制,可在保證性能指標值足夠接近最優性能值的同時,顯著地減少問題求解的計算量。實現次優控制的主要的途徑是把複雜的受控系統通過適當的方法化為兩個較為簡單的子受控系統,並且針對子系統來計算最優控制,再綜合地作必要的修正。實現系統分解的途徑有非奇異攝動方法和奇異攝動方法。對控制函數的修正需按期望性能指標值對最優性能值的接近程度來確定;要求接近的程度越高,修正計算量也就越大。特別是對於要求計算機實時控制的受控系統,為了避免過大的計算量或避免增加控制系統在組成上的複雜性,常常更宜採用次優控制以代替最優控制。
極大值原理不僅可用於解決連續形式的受控系統的最優控制問題,而且還被推廣於處理離散形式的受控系統的最優控制問題。離散最優控制問題的極大值原理稱為離散極大值原理。極大值原理對求解分佈參數系統的最優控制問題也很有效,相應的方法稱為分佈參數系統的極大值原理。