測量
測量
測量是按照某種規律,用數據來描述觀察到的現象,即對事物作出量化描述。測量是對非量化實物的量化過程。
在機械工程裡面,測量指將被測量與具有計量單位的標準量在數值上進行比較,從而確定二者比值的實驗認識過程。
1.測量的客體即測量對象:
主要指幾何量,包括長度、面積、形狀、高程、角度、表面粗糙度以及形位誤差等。由於幾何量的特點是種類繁多,形狀又各式各樣,因此對於他們的特性,被測參數的定義,以及標準等都必須加以研究和熟悉,以便進行測量。
2.計量單位:
我國國務院於1977年5月27日頒發的《中華人民共和國計量管理條例(試行)》第三條規定中重申:“我國的基本計量制度是米制(即公制),逐步採用國際單位制。”1984年2月27日正式公布中華人民共和國法定計量單位,確定米製為我國的基本計量制度。在長度計量中單位為米(m),其他常用單位有毫米(mm)和微米(μm)。在角度測量中以度、分、秒為單位。
3.測量方法:
指在進行測量時所用的按類敘述的一組操作邏輯次序。對幾何量的測量而言,則是根據被測參數的特點,如公差值、大小、輕重、材質、數量等,並分析研究該參數與其他參數的關係,最後確定對該參數如何進行測量的操作方法。
4.測量的準確度:
指測量結果與真值的一致程度。由於任何測量過程總不可避免地會出現測量誤差,誤差大說明測量結果離真值遠,準確度低。因此,準確度和誤差是兩個相對的概念。由於存在測量誤差,任何測量結果都是以一近似值來表示。
1、定類測量
定類測量也被稱為類別測量或定名測量,它是測量層次中最低的一種。
2、定序測量
定序測量也稱為等級測量或順序測量。定序測量的取值可以的按照某種邏輯順序將研究對象排列出高低或大小,確定其等級及次序。
3、定距測量
定距測量也稱為間距測量或區間測量。它不僅能夠將社會現象或是事物區分為為不同的類別、不同的級別,而且可以確定它們相互之間的間隔距離和數量差別。
4、定比測量
定比測量也稱為等比測量或比例測量。定比測量除了具有上述三種尺度的全部性質之外,還具有一個絕對的0點(有實際意義的0點)。
四種測量尺度的數學特性總結
| 定類測量 | 定序測量 | 定距測量 | 定比測量 | |
| 類別區分(=,=) | 有 | 有 | 有 | 有 |
| 次序區分(〉,〈) | 有 | 有 | 有 | |
| 距離區分(+,-) | 有 | 有 | ||
| 比例區分(×,÷) | 有 |

測量
開環測量系統與閉環測量系統:如圖所示。
測量
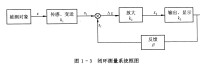
測量
測量誤差是測得值減去被測量的真值。
1.誤差的表示方法
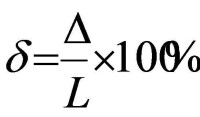
測量
絕對誤差可用下式定義:
Δ=x-L
式中:Δ——絕對誤差;
x——測量值;
L——真值。
採用絕對誤差表示測量誤差,不能很好說明測量質量的好壞。例如,在溫度測量時,絕對誤差Δ=1℃,對體溫測量來說是不允許的,而對測量鋼水溫度來說卻是一個極好的測量結果。
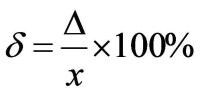
測量
相對誤差可用下式定義:如圖所示。
式中:δ——相對誤差,一般用百分數給出;
Δ——絕對誤差;
L——真值。
標稱相對誤差:如圖所示。
誤差的表示方法(3)
(3)引用誤差
測量
引用誤差是儀錶中通用的一種誤差表示方法。
(4)基本誤差
儀錶在規定的標準條件下所具有的誤差。
(5)附加誤差
儀錶的使用條件偏離額定條件下出現的誤差。
2.測量誤差的性質
(1)隨機誤差
對同一被測量進行多次重複測量時,絕對值和符號不可預知地隨機變化,但就誤差的總體而言,具有一定的統計,規律性的誤差稱為隨機誤差。引起的原因是測量過程中測量人員和測量設備的隨機因素造成的,在測量過程中是不可避免的,只能通過提高測量實施人員的測量技術技能,改善測量方法或提高測量儀器儀錶系統的精度來減少隨機誤差。
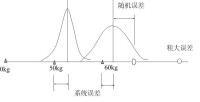
(2)系統誤差
測量
(3)粗大誤差
明顯偏離測量結果的誤差。引起的原因主要是測量環境突然改變或測量實施過程中的錯誤等不穩定、不可預測的原因造成的,一般在測量結果分析過程中予以剔除或忽略。
測量誤差的性質(2)如圖所示。
在幾何量測量中,按用途和特點可將它分為以下幾種:
實物量具
它是指在使用時以固定形態復現或提供給定量的一個或多個已知值的量具。如量塊、直角尺、各種曲線樣板及標準量規等。
極限量規
它是指一種沒有刻度的專用檢驗工具,用這種工具不能得出被檢驗工件的具體尺寸,但能確定被檢驗工件是否合格,如光滑極限量規、螺紋極限量規等。
顯示測量儀器
它是指顯示值的測量儀器。其顯示可以是模擬的(連續或非連續)或數字的,可以是多個量值同時顯示,也可提供記錄。如模擬電壓表、數字頻率計、千分尺等。
測量系統
它是指組裝起來進行特定測量的全套測量儀器和其它設備,測量系統可以包含實物量具。固定安裝著的測量系統稱為測量裝備。
幾何量測量儀器根據構造上的特點還可以分為以下幾種:
游標式測量儀器
微動螺旋副式測量儀器
如外徑千分尺、內徑千分尺及公法線千分尺等。
機械式測量儀器
如百分表、千分表、槓桿比較儀、扭簧比較儀及三坐標測量機等。
光學機械式測量儀器
如光學計、測長儀、投影儀、接觸干涉儀、干涉顯微鏡、光切顯微鏡、工具顯微鏡及測長機等。
氣動式測量儀器
如流量計式、氣壓計式等。
電學式測量儀器
如電接觸式、電感式、電容式、磁柵式、電渦流式及感應同步器等。
光電式測量儀器
如激光干涉儀、激光准直儀、激光絲桿動態測量、光柵式測量儀以及影像測量儀等。

測量儀器
直接測量:無需對被測量與其他實測量進行一定函數關係的輔助計算而直接得到被測量值的測量。
間接測量:通過直接測量與被測參數有已知函數關係的其他量而得到該被測參數量值的測量。
接觸測量:儀器的測量頭與工件的被測表面直接接觸,並有機械作用的測力存在(如接觸式三坐標等)。
非接觸測量:儀器的測量頭與工件的被測表面之間沒有機械的測力存在(如光學投影儀、氣動量儀測量和影像測量儀等)。
組合測量:如果被測量有多個,雖然被測量(未知量)與某種中間量存在一定函數關係,但由於函數式有多個未知量,對中間量的一次測量是不可能求得被測量的值。這時可以通過改變測量條件來獲得某些可測量的不同組合,然後測出這些組合的數值,解聯立方程求出未知的被測量。
比較測量:比較法是指被測量與已知的同類度量器在比較器上進行比較,從而求得被測量的一種方法。這種方法用於高準確度的測量。
零位法:被測量與已知量進行比較,使兩者之間的差值為零,這種方法稱為零位法。例如電橋、天平、桿秤、檢流計
偏位法:被測量直接作用於測量機構使指針等偏轉或位移以指示被測量大小。
替代法:替代發是將被測量與已知量先後接入同一測量儀器,在不改變儀器的工作狀態下,使兩次測量儀器的示值相同,則認為被測量等於已知量。例如曹沖稱象。
累積法:被測量的物體的量值太小,不能夠用測量儀器直接測量單一的物體,則測量相同規格的物體集合再求其平均值的方法,如測量一張紙張的厚度,一根頭髮絲的直徑,一顆訂書針的質量等
1.根據測量條件分為
(1)等精度測量:用相同儀錶與測量方法對同一被測量進行多次重複測量
(2)不等精度測量:用不同精度的儀錶或不同的測量方法,或在環境條件相差很大時對同一被測量進行多次重複測量
2.根據被測量變化的快慢分為
(1)靜態測量
(2)動態測量
1.直接測量法:不必測量與被測量有函數關係的其他量,而能直接得到被測量值的測量方法。
2.間接測量法:通過測量與被測量有函數關係的其他量來得到被測量值的測量方法。
3.定義測量法:根據量的定義來確定該量的測量方法。
4.靜態測量方法:確定可以認為不隨時間變化的量值的測量方法。
5.動態測量方法:確定隨時間變化量值的瞬間量值的測定方法。
6.直接比較測量法:將被測量直接與已知其值的同種量相比較的測量方法。
7.微差測量法:將被測量與只有微小差別的已知同等量相比較,通過測量這兩個量值間的差值來確定被測量值的測量方法。
(1)正態分佈
隨機誤差具有以下特徵:
①絕對值相等的正誤差與負誤差出現的次數大致相等——對稱性;
②在一定測量條件下的有限測量值中,其隨機誤差的絕對值不會超過一定的界限——有界性;
③絕對值小的誤差出現的次數比絕對值大的誤差出現的次數多——單峰性;
④對同一量值進行多次測量,其誤差的算術平均值隨著測量次數n的增加趨向於零——抵償性。(凡是具有抵償性的誤差原則上可以按隨機誤差來處理);
這種誤差的特徵符合正態分佈

測量
(3)用測量的均值代替真值;
(4)有限次測量中,算術平均值不可能等於真值;
(5)正態分佈隨機誤差的概率計算
當k=±1時,Pa=0.6827,即測量結果中隨機誤差出現在-σ~+σ範圍內的概率為68.27%,而|v|>σ的概率為31.73%。出現在-3σ~+3σ範圍內的概率是99.73%,因此可以認為絕對值大於3σ的誤差是不可能出現的,通常把這個誤差稱為極限誤差。
 測量 | 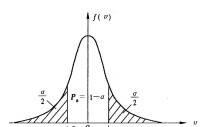 測量 |
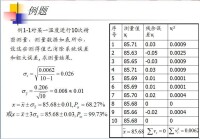
例題:見圖所示:
(6)不等精度直接測量的權與誤差
1.在不等精度測量時,對同一被測量進行m組測量,得到m組測量列(進行多次測量的一組數據稱為一測量列)的測量結果及其誤差,它們不能同等看待。精度高的測量列具有較高的可靠性,將這種可靠性的大小稱為“權”。
2.“權”可理解為各組測量結果相對的可信賴程度。測量次數多,測量方法完善,測量儀錶精度高,測量的環境條件好,測量人員的水平高,則測量結果可靠,其權也大。權是相比較而存在的。權用符號p表示,有兩種計算方法:?
①用各組測量列的測量次數n的比值表示,並取測量次數較小的測量列的權為1,則有
p1∶p2∶…∶pm=n1∶n2∶…∶nm
②用各組測量列的誤差平方的倒數的比值表示,並取誤差較大的測量列的權為1,則有
p1∶p2∶…∶pm=(1/σ1)^2:(1/σ2)^2:(1/σ3)^2:……(1/σm)^2
 測量 |  測量 |
(1)系統誤差產生的原因
①感測器、儀錶不準確(刻度不準、放大關係不準確)
②測量方法不完善(如儀錶內阻未考慮)
③安裝不當
④環境不合
⑤操作不當;
(2)系統誤差的判別
①實驗對比法,例如一台測量儀錶本身存在固定的系統誤差,即使進行多次測量也不能發現,只有用更高一級精度的測量儀錶測量時,才能發現這台測量儀錶的系統誤差;

測量
③準則檢驗法
馬利科夫判據是將殘餘誤差前後各半分兩組,若“Σvi前”與“Σvi后”之差明顯不為零,則可能含有線性系統誤差。
阿貝檢驗法則檢查殘餘誤差是否偏離正態分佈,若偏離,則可能存在變化的系統誤差。將測量值的殘餘誤差按測量順序排列,且設A=v12+v22+…+vn2,B=(v1-v2)2+(v2-v3)2?+…+(vn-1-vn)2+(vn-v1)2。
若|B/2A-1|>1/n^1/2,則可能含有變化的系統誤差。
(3)系統誤差的消除
在測量結果中進行修正已知系統誤差,變值系統誤差,未知系統誤差
消除系統誤差的根源 根源
在測量系統中採用補償措施
實時反饋修正
剔除壞值的幾條原則:
(1)3σ準則(萊以達準則):如果一組測量數據中某個測量值的殘餘誤差的絕對值|vi|>3σ時,則該測量值為可疑值(壞值),應剔除。

測量
(3)格拉布斯準則:某個測量值的殘餘誤差的絕對值|vi|>Gσ,則判斷此值中含有粗大誤差,應予剔除。G值與重複測量次數n和置信概率Pa有關。
測量

測量
絕對誤差的合成(例題):
用手動平衡電橋測量電阻RX。已知R1=100Ω,R2=1000Ω,RN=100Ω,各橋臂電阻的恆值系統誤差分別為ΔR1=0.1Ω,ΔR2=0.5Ω,ΔRN=0.1Ω。求消除恆值系統誤差后的RX.

測量
推導過程,如圖冊所示:
最小二乘法應用例子:如圖冊所示:
5.用經驗公式擬合實驗數據——回歸分析

最小二乘法推出過程
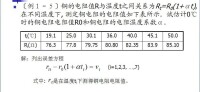
最小二乘法應用例子
測量單位Unit of measurement
把測量中的標準量定義為“單位”。單位是一個選定的標準量,獨立定義的單位稱“基本單位” (Base unit );由物理關係導出的單位稱“導出單位”(Derived unit)。
國際單位制(SI)International System of Units
1980年由國際計量大會(CGPM)採納和推薦的一種一貫單位制。註:SI是國際單位制的國際通用符號。
2013年,國際單位制下7個基本單位:
長度:米 m
質量:千克(公斤) kg
時間:秒 s
電流 安[培] A
熱力學溫度:開[爾文] k
物質的量:摩[爾] mol
發光強度:坎[德拉]cd
正確讀出刻度尺的零刻度、最小刻度(最小分度值)、測量範圍(量程);
把刻度尺的刻度儘可能與被測物體接近,不能歪斜;
讀數時,視線應垂直於被測物體與刻度尺;
讀出最小刻度以上各位數字;
記錄的測量數據,包括準確值、估計值以及單位(沒有單位的數值是毫無意義的)
對於精密測量,要注意:
要考慮測量溫度及濕度對測量結果的影響,量具和被測工件應儘可能放在同一環境溫度中,1m以下不少於1.5h,1~3m的為3h,超過3m時應在4h以上。
要減小視力引起的誤差。一般常用多次測量求平均值的辦法減小誤差。
測量周圍環境要求:無震動、無磁場、無粉塵等。
