無偏估計

無偏估計量，數學期望等於被估計的量的統計估計量。

設^θ(X1,X2,…,Xn)是θ的估計量，若E(^θ)=θ，對一切θ∈Θ，則稱^θ為θ的無偏估計量，否則稱為θ的有偏估計量。

無偏估計量的定義是：設（ξ∧）是ξ的一個估計量，若E（ξ∧）=ξ ，則稱ξ∧是ξ的無偏估計量 下面說明題目中的四個估計量都是λ的無偏估計量。因為ξ8、ξ8、ξ8 都是取自參數為λ的泊松總體的樣本。

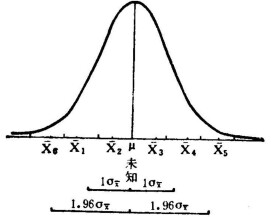
對於待估參數，不同的樣本值就會得到不同的估計值。這樣，要確定一個估計量的好壞，就不能僅僅依據某次抽樣的結果來衡量，而必須由大量抽樣的結果來衡量。對此，一個自然而基本的衡量標準是要求估計量無系統偏差。也就是說，儘管在一次抽樣中得到的估計值不一定恰好等於待估參數的真值，但在大量重複抽樣時，所得到的估計值平均起來應與待估參數的真值相同，換句話說，希望估計量的均值（數學期望）應等於未知參數的真值，這就是所謂無偏性(Unbiasedness)的要求。

下面說明題目中的四個估計量都是λ的無偏估計量。首先，因為ξ1、ξ2、ξ3 都是取自參數為λ的泊松總體的樣本，獨立同分佈，所以它們的期望和方差都是λ ，則

（1）無偏性E（λ1∧）= E（ξ1）= λE（λ2∧）= E[(ξ1+ξ2)/2]= (λ+λ)/2 = λE（λ3∧）= E[(ξ1+2*ξ2)/3]= (λ+2λ)/3 = λE（λ4∧）= E[(ξ1+ξ2+ξ3)/3]= (λ+λ+λ)/3 = λ

（2）有效性，即最小方差性D（λ1∧）= D（ξ1）= λD（λ2∧）= D[(ξ1+ξ2)/2]= [D(ξ1)+D(ξ2)]/4= (λ+λ)/4 = λ/2D（λ3∧）= D[(ξ1+2*ξ2)/2]= [D(ξ1)+4D(ξ2)]/9= (λ+4λ)/9 = 5λ/9D（λ4∧）= D[(ξ1+ξ2+ξ3)/3]= [D(ξ1+ξ2+ξ3)]/9 =(λ+λ+λ)/9 = λ/3其中 D（λ4∧）= λ/3 最小，所以無偏估計量 λ4∧最有效。