布拉伐格子

把基元以相同的方式放置在每個格點上，就得到實際的晶體結構。基元只有一個原子的晶格稱為布拉菲格子。若基元由兩個或兩個以上的原子構成，此時的晶體結構可看成是由兩個或兩個以上相同的布拉菲格子套構而成。

在晶體中，由格矢量 Rn = n1 a1+n2 a2+n3 a3 的全部端點(格點)的集合 (ni為0和正負整數) 即構成一個空間格子，它反映了晶格的周期性。晶格的周期性可以表示為一個晶格經過平移操作后與原來晶格完全重合。通常情況下，具有平移對稱性的格子就稱為布拉伐格子。這種微觀的平移對稱性可導致宏觀上的其他對稱性，包括轉動，鏡面，反演點對稱性。 Rn稱為布拉伐格子的格矢； a1、 a2、 a3是三個不共面的矢量, 稱為布拉伐格子的基矢。

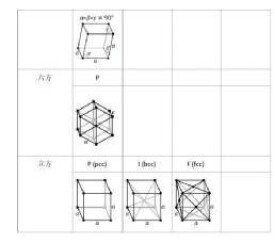
布拉伐格子是晶格的一種數學抽象，其中布拉伐格子的所有格點都是幾何位置上等價、周圍環境相同的點；若把原子或原子團安置在布拉伐格子的每一個格點上，就可得到相應的晶格。雖然晶格的類型很多，但自然界中的布拉伐格子卻只有14種。這14種布拉伐格子又可劃分為七大晶系。

七大晶系分別是：單斜晶系、三斜晶系、三角晶系、四方晶系、正交晶系、六角晶系、立方晶系