加法交換律

數學計算的法則之一

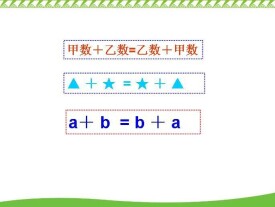
加法交換律是數學計算的法則之一。指兩個加數相加，交換加數的位置，和不變。

交換律是二元運算的一個性質，意指在一個包含有二個以上的可交換運運算元的表示式，只要運算元沒有改變，其運算的順序就不會對運算出來的值有影響。

目錄

1定義 2局限性 3相關定律

定義

在兩個數的加法運算中，在從左往右計算的順序，兩個加數相加，交換加數的位置，和不變。例如：

字母：

數字：

局限性

儘管這一定律看上去似乎對於任何事物都顯然成立，但事實並非如此。在沒有時間的空間下（三維以內），加法交換律是完全正確的。但是一旦有了時間軸，這個定律就不成立了。

證明這個理論的實驗之一如下：

(1)取一個方體物體，如較厚的書或者魔方之類皆可。將其平放在水平台上。

(2)現令正對上方的一面，平行與桌面對著你的一面和平行桌面在你右邊的面為面一、二、三。各自相對的面為面四五六。

(3)定義操作a為將此長方體翻轉180度。即面三、六不動，一四交換，二五交換。定義操作b為將左邊的面翻至上方。

(4)執行a+b后，向上的一面為面六。執行后，向上的一面為面三。顯然不等於。

此外對於無窮多個數相加，使用加法交換律，結果可能是錯誤的。

下面展示的是數列的無窮求和。

但是，通過觀察，原式應該至少是一個大於的數。

相關定律

加法結合律：

乘法交換律：

乘法結合律：

乘法分配律：

減法的性質：

除法的性質：

商不變性質：

目錄