反射變換
歐氏幾何中的變換
定義1
1.平面上的反射變換
設l為平面上一直線,將平面上任一點P變換到關於l與它對稱的點P'的變換,叫做平面上關於直線l的反射變換;
設A為平面上一點,將平面上任一點P變換到關於點A與P對稱點p'的變換,叫做平面上關於點A的反射變換。
2.空間中的反射變換
設為空間中一平面,將空間任一點P變換到關於平面與P對稱的點P'的變換,稱做空間關於平面的反射變換。
設A為空間中一點,將空間任一點P變換到關於點A與P對稱的點P'的變換,叫做空間關於點A的反射變換。
定義2
我們通常稱集合A到自身的映射f是集合A上的 變換,即。若是一一映射,則稱是集合A上的一一變換。
設是平面上的定直線,S是平面上的變換,P、P'是一對對應點。如果線段PP'被直線垂直平分,那麼稱S為 反射變換(symmetric transformation),簡記為,為反射軸。
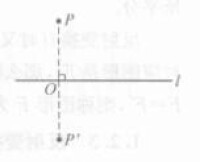
圖1
由此可知,反射變換由反射軸或一對對應點確定。
在反射變換S(l)下,點P變換為點P',圖形F變換為圖形F',這可表示為
或記為
性質1 反射變換下兩點之間距離不變,即對於任意兩點P、Q,,則1(圖3)。
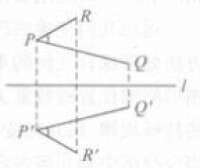
圖3
說明 性質1和性質2分別揭示了反射變換的保距性和保角性,並由此可以得到:任一圖形F,經反射變換后得到F',則F與F'全等。
顯然,我們有
性質3 在反射變換下,反射軸是不動點的集合,垂直於反射軸的直線是不變直線。
性質4 設O為反射軸上一點,P、P’是一對對應點,則被所平分。
反射變換有時又稱為 軸對稱變換,如果一個圖形F在軸對稱變換下的對應圖形是,那麼稱是F的軸對稱圖形,它們是互為軸對稱圖形,又若,則稱圖形F為軸對稱變換下的自對稱圖形,如圖2(2) 。
反射變換可以組成集合,我們在這樣的集合中定義“乘法運算”,即運算“ ”:
設兩個反射變換,若一個點P(或一個圖形F)在反射變換下為點(或圖形),而點(或圖形F')在反射變換下為點(或圖形),則稱點P(或圖形F)在反射變換與的乘積變換下為點P''(或圖形F"),簡記為,而變換稱為與的乘積變換。
