比熵
比熵
熵是工程熱力學中的一個狀態參數。熵的變化表徵了可逆過程中熱交換的方向和大小。熵的變化只與其始末狀態有關,與達到這一狀態的過程無關。當系統的熵增大時,系統從外界吸熱。當系統的熵減小時,系統對外界放熱。而1kg工質的熵,便是比熵。
1824年法國工程師卡諾在熱機效率進行深入研究的基礎上,提出了著名的卡諾定理。其表述如下:
定理一:在相同的高溫熱源和低溫熱源間工作的一切可逆熱機具有相同的熱效率,與工質的性質及循環形式無關。
定理二:在相同的高溫熱源和低溫熱源間工作的一切不可逆熱機的熱效率,都小於可逆熱機的熱效率。
根據卡諾定理,在溫度分別為 和 的恆溫熱源間工作的一切可逆熱機的熱效率都相同,即
即式中, 、均為絕對值,如果改為代數值, 應為負值,於是上式可寫為:
說明,在卡諾循環中,工質與熱源交換的熱量除以熱源的熱力學溫度所得的商的代數和等於零。
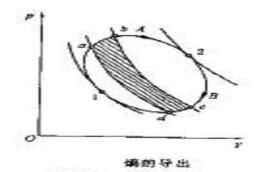
可以證明,以上結論適用於任何可逆循環。圖1示出的是一個任意可逆循環,假設用一組可逆絕熱線將其分割成無數個微元循環。對於每個微元循環(如圖a-b-c-d-a)可認為是由兩個可逆定溫過程和兩個可逆絕熱過程組成的微元卡諾循環,根據上面分析的所得式,則有:對全部微元卡諾循環積分,可得式中、 ——代表微元循環與熱源交換的熱量,本身為代數值,由於含義相同,可統一用表示;
、 ——分別為微元循環的熱源溫度,統一用T來表示,於是上式可寫為:
即稱為克勞休斯積分等式。它表明,工質經任意可逆循環后, 沿整個循環的積分為零。
由上式可知, 具有狀態參數的特性,因此, 必定是一狀態參數。1865年克勞休斯將這一狀態參數定名為熵,以符號S表示,單位為J/K,於是對於1kg的工質,式可寫成式中 、 ——下標是強調或必須是可逆過程的換熱量;
T——熱源的熱力學溫度,既然是可逆過程,當然也是工質的熱力學溫度。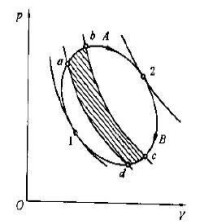

圖1