關鍵路徑法
關鍵路徑法
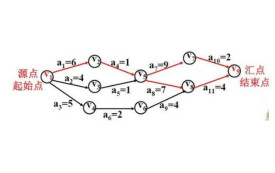
關鍵路徑法(Critical Path Method,CPM)是一種基於數學計算的項目計劃管理方法,是網路圖計劃方法的一種,屬於肯定型的網路圖。關鍵路徑法將項目分解成為多個獨立的活動並確定每個活動的工期,然後用邏輯關係(結束-開始、結束-結束、開始-開始和開始結束)將活動連接,從而能夠計算項目的工期、各個活動時間特點(最早最晚時間、時差)等。在關鍵路徑法的活動上載入資源后,還能夠對項目的資源需求和分配進行分析。關鍵路徑法是現代項目管理中最重要的一種分析工具。
關鍵路徑法
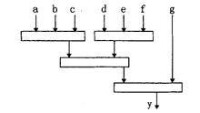
箭線圖(ADM)法又稱為雙代號網路圖法,它是以橫線表示活動而以帶編號的節點連接活動,活動間可以有一種邏輯關係,結束-開始型邏輯關係。
在箭線圖中,有一些實際的邏輯關係無法表示,所以在箭線圖中需要引入虛工作的概念。
關鍵路徑法
非常重要的,除了箭線圖(ADM)本身具有正確的邏輯性,良好的繪圖習慣也是必要的。因此在繪圖時遵守上面的這些規則就是非常重要的,另外,在繪圖時,一般盡量使用直線和折線,在不可避免的情況下可以使用斜線,但是要注意邏輯方向的清晰性。
繪製箭線圖時主要有以下一些規則:
⒈在箭線圖(ADM)中不能出現迴路。如上文所述,迴路是邏輯上的錯誤,不符合實際的情況,而且會導致計算的死循環,所以這條規則是必須的要求。
⒉箭線圖(ADM)一般要求從左向右繪製。這雖然不是必須的要求,但是符合人們閱讀習慣,可以增加箭線圖(ADM)的可讀性。
⒊每一個節點都要編號,號碼不一定要連續,但是不能重複,且按照前後順序不斷增大。這條規則有多方面的考慮,在手工繪圖時,它能夠增加圖形的可讀性和清晰性,另外,在使用計算機運行箭線圖(ADM)這一條就非常重要,因為在計算機中一般通過計算節點的時間來確定各個活動的時間,所以節點編號不重複是必須的。
⒋一般編號不能連續,並且要預留一定的間隔。主要是為了在完成的箭線圖(ADM)中可能需要增加活動,如果編號連續,新增加活動就不能滿足編號由小到大的要求。
⒌表示活動的線條不一定要帶箭頭,但是為了表示的方便,一般推薦使用箭頭。這一條主要是繪製箭線圖(ADM)時可以增加箭線圖(ADM)的可讀性。
⒍一般要求雙代號網路圖要開始於一個節點,並且結束於一個節點。此要求可以在手工繪圖增加可讀性,而在計算機計算時,可以增加效率和結果的清晰性。
⒎在繪製網路圖時,一般要求連線不能相交,在相交無法避免時,可以採用過橋法或者指向法等方法避免混淆。此要求主要是為了增加圖形的可讀性。
關鍵路徑法
他們聯繫了雷明頓蘭德(Remington Rand)公司的Macuchy 博士,幫他們解決計算機使用的問題,後者派出了年輕的數學家James E. Kelly去協助杜邦(Du Pont)公司解決問題,杜邦公司方面的負責人是Morgan Walker。
他們要解決的問題是在工程項目中工期和費用之間的關係,他們研究的是如何能夠採取正確的措施,在減少工期的情況下能儘可能少的增加費用。1957年5月7日,在特拉華州內瓦克召開的一個會議正式確定開始新計劃技術的開發。Kelly借用了線性規劃的概念來解決項目計劃自動計算的問題,簡單的說就是確定了每個活動的工期和活動間的邏輯關係,輸入電腦後就能自動計算項目的工期,為了電腦的計算,Kelly在活動間使用了i,j這樣的節點來表示活動間的前後邏輯關係。
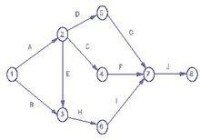
當時遇到的一個問題是,杜邦公司的管理層並不理解Kelly所使用的方法,為了讓其他人能夠理解所使用方法的原理,Kelly就繪製了圖形來解釋電腦所作的工作,圖形以箭線表示活動,以節點表示活動間的邏輯關係,這就是最早的箭線圖(ADM)。
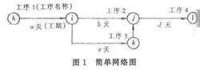
關鍵路徑法
內,關鍵路徑法主要還是用於進度的計劃和控制方面。Kelly和Walker還提出了資源載入和分配的方法,當然也存在和費用分析一樣的問題。
儘管存在這些問題,在1957年7月24日,他們已經做了一個簡化的例子,稱為”George Fischer Works”,這個計劃包括了61條活動,其中有8個時間限制和16條虛工作。在剛開發出這種方法時,他們將這種方法稱為Kelly-Walker法,而計劃中的關鍵線路,他們稱之為主鏈路(Main chain)。
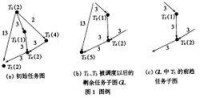
關鍵路徑法
1958年,他們進行了第二次試驗,此試驗所針對的是一個價值2000萬美元的化學設備項目,根據Kelly和Walker在1959年發表的論文,此次試驗顯示的最主要的優點是能夠比較容易的包含設計部分的計劃。
不過現在人們最常提及的一個試驗是他們隨後進行的維護設備的試驗,在此項目中,他們使用Kelly-Walker法進行分析和計劃,使得設備維護時間減少了25%。
1959年,Kelly和Walker共同發表了”Critical Path Planning and Scheduling”論文,在這篇長達25頁的論文中,Kelly和Walker不僅闡述了關鍵路徑法的基本原理,還提出了資源分配與平衡,費用計劃的方法。我們今天所使用的方法的原理,與Kelly和Walker在論文中提出的方法,並沒有原則上的不同。
不過隨後關鍵路徑法的發展並不是很順利,杜邦公司開發此項技術的領導層更換之後,不再使用這項技術,而雷明頓蘭德公司也認為這項技術沒有太大前途。
對於關鍵路徑法的發展起到重要作用的是Mauchly博士和Kelly隨後成立的Mauchly合夥公司。在60年代初期,在Kelly的帶領下,此公司進行了大量的關鍵路徑法的培訓和推廣工作。
與此同時,另外一個對關鍵路徑法(CPM)的發展起到重要作用的是美國海軍北極星計劃開發的計劃評審技術(PERT)。在1955年11月17日,美國海軍北極星計劃成立了一個特別項目管理辦公室(SPO),管理其Fleet Ballistic Missile計劃,負責人是Admiral Raborn。在1956年和1957年期間,他們研究了各種已經存在的項目管理技術,在大約1957年秋季的時候,他們接觸到了杜邦公司開發的計劃管理技術,這對他們開發PERT起到了重要的作用。1958年1月份,SPO研究了在計算機上實現計劃和控制的可行性,1958年1月27日,SPO正式成立了一個小組開發PERT技術,在大約一年以後,PERT技術成為一種可操作性的技術,計劃評審技術(PERT)和關鍵路徑法(CPM)基本上一樣,唯一的區別是計劃評審技術的每個活動的工期不是確定的,而是包括了悲觀值,樂觀值和最有可能值三個值。比較有趣的是,1959年,北極星計劃的這個特別項目管理辦公室(SPO)開了一個招待會,介紹他們的這種新技術,並希望參會者能給出更多的意見,Kelly和Walker在被邀請之列,在會上,他們發現SPO開發的PERT和他們的Kelly-Walker法原理上完全一樣,而SPO所說的關鍵線路(Critical Path),就是他們的Kelly-Walker法中的主鏈路(Main Chain)。回去之後,他們決定將它們的方法的名稱改為關鍵路徑法(Critical Path Method)。
在60年代初期,PERT的發展比較迅速,據統計,到1964年,關於PERT的參考書目和論文達到了1000多種。到1961年,各種基於PERT的類似的方法出現,如PERT/Cost,PERT-RAMPS(Resource Allocation & Multi-Project Schedule),MAPS,SCANS,TOPS,PEP,TRACE,LESS和PAR等。其中PEP法是將甘特圖的活動賦以邏輯關係,這是計劃軟體一般採用的一種圖形輸出方法。1962年的時候,時任美國國防部長MacNamara在起草一項法令時,指出計劃評審法和關鍵路徑法同時並存的局面容易引起混淆,以後國防部的所有部門一律使用計劃評審法(PERT),這在當時對於關鍵路徑法的提倡者是一個重大打擊,不過在隨後的發展中,關鍵路徑法(CPM)逐漸佔了優勢,真正使用計劃評審法的其實已經很少。而且即使是在當時,很多所謂的計劃評審法(PERT),其實質其實是關鍵路徑法(CPM)。如美國航空局(NASA)當時使用的NASA-PERT,實際就是關鍵路徑法(CPM)。
無論是關鍵路徑法(CPM)還是計劃評審法(PERT),最初使用的表示方法都是箭線法(ADM),在之後很長的一段時間箭線法(ADM)都是人們主要使用的方法,直到70年代以後,前導圖(PDM)才開始逐漸流行起來,但是箭線法(ADM)仍然使用極為廣泛。在90年代以後,美國Primavera公司開發出其Windows版本的計劃管理軟體時,只採用前導圖(PDM)作為其計算平台,從根本上改變了這一局面,從此以後,前導圖(PDM)成了人們主要使用的方法,而箭線圖(ADM)則很少使用。
在早期對於前導圖(PDM)的發展起到重要作用的是美國斯坦福大學的John W. Fondahl,他是60年代初期的非計算機關鍵路徑法的權威,1961年他發表了一篇題為”A Non-computer Approach to Critical Path Methods for the Construction Industry”,在這篇論文中,他闡述了前導圖系統,並把它作為一種效率比較高的手工繪製關鍵路徑法的方法,因為當時使用計算機運行CPM是非常昂貴的。Fondahl從1958年開始作為斯坦福大學的成員,受美國海軍委託為其研究提高生產效率的方法。其中最主要的成果就是這份論文,這份論文當時一共出售了20000份。
在這份論文中,根據習慣使用的流程圖方法,Fondahl提出了以節點表示活動以連接線表示活動間的邏輯關係。論文論述了流程圖的簡易性和使用手算在較少的人力投入下採用關鍵路徑法的可能性,同時論文也論述了費用工期互為反比的問題。斯坦福大學之後繼續研究了前導圖(PDM)的手工進度更新的問題,並在1964年發表了相關的技術報告。
雖然Fondahl博士極力強調他提出的方法是為了手工計算關鍵路徑法,但是H.B Zachry公司在1962年開始研究將前導圖法用於計算機上,1963年3月他們與IBM公司聯合進行該項研究,之後形成了IBM的計劃軟體,名為”Project Control System(PCS)”。該系統還是第一個在計劃中引入時間間隔(LAG)的軟體。雖然前導圖法最初被應用於大型機,但是隨後被廣泛應用於小型機和個人電腦上的軟體,這一趨勢使得前導圖(PDM)逐漸成為主要使用的方法,在國外前導圖(PDM)基本已經成為唯一在使用的方法,而箭線圖(ADM)只有在教學和培訓中還有時用到。而發展勢頭曾一度壓過關鍵路徑法(CPM)的計劃評審技術(PERT),正在使用的已經很少了。
在美國發展出關鍵路徑法(CPM)和計劃評審技術(PERT)的同時,其它一些國家如歐洲和英國等,也曾經開發出一些類似的項目管理技術,但是關於這些技術的記載已經很少。
關鍵路徑法(CPM)最初被開發是用於項目管理,不過,在發展過程中,它逐漸在工程項目的合同索賠和糾紛解決上起到重要作用。最早在訴訟中涉及到要求使用關鍵路徑法(CPM)是1972(Appeal of Minmar Builders,Inc,GSBCA No. 3430,72-2 BOA)年,在此案例中,法庭由於承包商沒有使用關鍵路徑法(CPM)而拒絕了承包商的索賠,因為其使用的橫道圖不能顯示具體的活動是否在關鍵線路上,從而無法判斷活動耽誤對於整體的影響。之後,關鍵路徑法(CPM)逐漸成為工期延誤索賠中必須的做法,並逐漸形成了很多專門的分析方法,甚至有很多人專業從事工期延誤分析的工作。
在關鍵路徑法中,一般有以下一些時間參數:
最早開始時間(Early Start)活動最早開始時間由所有前置活動中最後一個最早結束時間確定。
最早結束時間(Early Finish)活動的最早結束時間由活動的最早開始時間加上其工期確定。
最遲結束時間(Late Finish)一個活動在不耽誤整個項目的結束時間的情況下能夠最遲結束的時間。它等於所有緊后工作中最早的一個最晚開始時間。
最遲開始時間(Late Start)一個活動在不耽誤整個項目的結束時間的情況下能夠最遲開始的時間。它等於活動的最遲結束時間減去活動的工期。
總時差(Total Float) 指一項活動在不影響整體計劃工期的情況下最大的浮動時間。
自由時差(Free Float)指活動在不影響其緊后工作的最早開始時間的情況下可以浮動的時間。
如果是對於箭線圖法,用到的時間參數還常有:
最早節點時間(Early Event Occurrence Time)最早節點時間由其前置活動中最晚的最早結束時間確定。
最遲節點時間(Late Event Occurrence Time)最遲節點時間由其後置活動中最早的最遲開始時間確定。
在進行計算時,箭線圖和前導圖的計算過程有所不同。
箭線圖(ADM)的計算一般有正推法(Forward Pass)和逆推法(Backward Pass)兩種,正推法用於計算活動和節點的最早時間,其演演算法如下:
關鍵路徑法
⒉選擇一個開始於第一個節點的活動開始進行計算。
⒊令活動最早開始時間等於其開始節點的最早時間。
⒋在選擇的活動的最早開始時間上加上其工期,就是其最早結束時間。
⒌比較此活動的最早結束時間和此活動結束節點的最早時間。如果結束節點還沒有設置時間,則此活動的最早結束時間就是該結束節點的最早時間;如果活動的結束時間比結束節點的最早時間大,則取此活動的最早結束時間作為節點的最早時間;如果此活動的最早結束時間小於其結束節點的最早時間,則保留此節點時間作為其最早時間。
⒍檢查是否還有其它活動開始於此節點,如果有,則回到步驟3進行計算;如果沒有,則進入下一個節點的計算,並回到步驟3開始,直到最後一個節點。
活動和節點的最遲時間採用逆推法(Backward Pass)計算,逆推法(Backward Pass)一般從項目的最後一個活動開始計算,直到計算到第一個節點的時間為止,在逆推法的計算中,首先令最後一個節點的最遲時間等於其最早時間,然後開始計算,具體的計算步驟如下所示:
⒈設置最後一個節點的最遲時間,令其等於正推法計算出的最早時間。
⒉選擇一個以此節點為結束節點的活動進行計算。
⒊令此活動的最遲結束時間等於此節點的最遲時間。
⒋從此活動的最遲結束時間中減去其工期,得到其最遲開始時間。
⒌比較此活動的最遲開始時間和其開始節點的最遲時間,如果開始節點還沒有設置最遲時間,則將活動的最遲開始時間設置為此節點的最遲時間,如果活動的最遲開始時間早於節點的最遲時間,則將此活動的最遲開始時間設置為節點的最遲時間,如果活動的最遲開始時間遲於節點的最遲時間,則保留原節點的時間作為最遲時間
⒍檢查是否還有其它活動以此節點為結束節點,如果有則進入第二步計算,如果沒有則進入下一個節點,然後進入第二步計算,直至最後一個節點。
⒎第一個節點的最遲時間是本項目必須要開始的時間,假設取最後一個節點的最遲時間和最早時間相等,則其值應該等於1。
上面介紹了活動的最早和最遲時間的計算方法,以上的過程可以用比較簡單的公式來表達。
上面所講述的方法,我們一般稱為節點計演演算法,節點和活動的最早時間按照正推法進行計算,起點節點未規定時間時,我們取其時間為1,即
ETi=1(i=1)
對於任意一個節點,如果其之前只有一條活動時,則其最早時間按照下式計算,
ETj= ETi+Di-j
關鍵路徑法
ETj= max{ETi+Di-j}
其中Di-j為活動i-j的工期
對於活動的最早時間,最早開始時間為:
ESi-j=ETi
最早結束時間為
EFi-j= ESi-j+ Di-j
計劃的總工期
T=ETn-1
節點和活動的最遲時間以逆推法計算,計算時,首先令最後一個節點的最遲時間等於其最早時間,即
LTn=ETn
對於其之後只有一條活動的節點,最遲時間如下式所示
LTi=LTj-Di-j
對於其之後有多條活動的節點,最遲時間如下式所示
LTj=min{ LTj-Di-j}
工作i-j的最遲完成時間以下式計算,
LFi-j=LTj
最遲開始時間為
LSi-j=LFj- Di-j
以上的演演算法是節點計演演算法,另外,也可以採用一種叫做工作計演演算法的方法進行活動時間的計算,具體如下。
對於最早時間,採用正推法計算。在沒有指定節點的開始時間時,則起點開始活動的最早開始時間定為1,即
ESi-j=1
關鍵路徑法
ESi-j=ESh-i+ Dh-i
當工作i-j有多條緊前工作時,其最早開始時間按照以下公式計算
ESi-j=max {ESh-j+ Dh-i}
工作i-j的最早完成時間按照下式計算
EFi-j=ESi-j+ Di-j
網路計劃的計算工期按照下式確定
T=max {EFi-n}-1
活動的最遲結束時間和最遲開始時間需要採用逆推法計算。
以終點節點為箭頭節點的活動的最遲完成時間按照網路計劃的工期確定,即
LFi-j=T+1
其它活動的最遲開始時間按照下式計算
LFi-j=min {LFj-k- Dj-k}
活動的最遲開始時間以下式確定
LSi-j=LFi-j- Di-j
對於總時差和自由時差可以採用如下的公式計算。
總時差可以按照下式計算:
TFi-j= LSi-j- ESi-j
或者
TFi-j= LFi-j- EFi-j
當工作i-j有緊后工作j-k時,自由時差可以按照下式計算:
FFi-j=ESi-k- ESi-j- Di-j
或者
FFi-j=ESj-k-EFi-j
由於引入了多種邏輯關係,前導圖(PDM)的時間計算和箭線圖(ADM)有一些差別。除了前導圖(PDM)中不存在節點最早時間和最遲時間,在箭線圖(ADM)中提及的其它時間參數也都適合前導圖(PDM)。
對於活動的最早開始和最早結束時間,採用正推法計算,其演演算法如下所示:
⒈將第一個活動的最早開始時間設置為1.
⒉在活動的最早開始時間上加上其工期,得到活動的最早結束時間。
⒊根據該活動與後置活動的邏輯關係,計算後置活動應該的最早開始時間,並與其已有的最早開始時間對比,如果其後置活動還沒有設置最早開始時間,則將此時間設為其最早開始時間,如果此時間早於其後置活動已有的最早開始時間,則保留後置活動的原有最早開始時間,如果此時間遲於其後置活動已有的最早開始時間,則將此時間設置為後置活動的最遲開始時間。
⒋重複步驟2和3,直到所有活動的時間被計算完為止。
對於以上所示的最早時間的計算過程,可以以公式的形式表示如下:
當活動間的邏輯關係為SS,則計算如下
ESj=max{ ESi+ STS}
當活動間的邏輯關係為FS,則計算如下
ESj= max{ESi+ Di+ FTS}
當活動間的邏輯關係為FF,計算如下
ESj= max{ESi+ Di- Dj+FTF}
當活動間的邏輯關係為SF,計算如下
ESj=max{ ESi- Dj+STF}
在計算出各個活動的最早開始和結束時間之後,就可以計算活動的自由時差,在計算前導圖(PDM)的自由時差時應注意,由於引入了多種邏輯關係,並且活動間可以存在延時,所以其計算方法與箭線圖(ADM)的計算方法不一樣。
對於前導圖(PDM)的活動間,除了延時還可以存在時間間隔(LAG),一般可以按照下面的方式計算。
當活動間的邏輯關係為SS,則計算如下
LAGi-j= ESj- ESi- STS
當活動間的邏輯關係為FS,則計算如下
LAGi-j= ESj- EFi- FTS
當活動間的邏輯關係為FF,計算如下
LAGi-j= EFj- EFi- FTF
當活動間的邏輯關係為SF,計算如下
LAGi-j= EFj- ESi- STF
則對於任意一個活動,其自由時差為
FFi=min{ LAGi-j}
最後一個活動的自由時差為0.
對於總時差,終點節點的總時差為0,對於其它任意一個節點,總時差按照下式進行計算
TFi=min{TFj+ LAGi-j}
對於任意一個活動的最晚開始時間可以由其最早開始時間加上總時差得到,同樣,其最晚開始時間可以由最早結束時間加上其總時差得到,公式表示如下
LSi=ESi+TFi
LFi=EFi+TFi