酶動力學

研究酶催化劑參與的生物反應過程中，酶反應速率及影響酶反應速率的各種因素。它能提出底物到產物之間可能歷程與機理，獲取反應速率和影響此速率的諸因素，例如溫度、pH、反應物系的濃度以及有關抑製劑等的關係，以滿足酶反應過程開發和生物反應器設計的需要。

底物濃度的影響 長期以來，人們已經知道許多化學反應的速率隨著反應物濃度的增加而增加。對於一個單底物不可逆的酶反應，當底物濃度增加時，酶反應的速率不斷增大並接近一個最大值（見圖）。 L.米歇利斯和L.M.門騰（1913）基於酶被底物飽和的現象，提出“中間產物”學說：即酶（E）與底物（S）結合形成一個不穩定的中間產物或絡合物（ES），然後生成產物（P）和遊離酶E，並推導出反應速率與底物濃度的關係式(2),即米氏方程式。它是研究影響反應速率各種因素的基本動力學的方程式，式中 r為反應速率，亦即酶活力,以單位時間內底物被分解的量來表示， r=-d S/d t； S表示底物濃度; rmax為最大反應速率； Km為米氏常數， Km=（ k2+ k3）/ k1,其數值等於當酶反應速率為最大反應速率一半時的底物濃度。 Km是酶的一個特徵性常數，當速率常數 K2比 K3大很多時, Km就接近絡合物（ES）的解離常數。因此， Km是酶與底物親和力的量度: Km值高表示E與S的親和力弱; Km值低時表示親和力強。

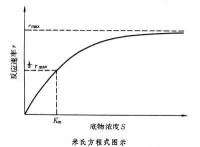
在米氏方程中，有兩個基本常數 Km和 rmax，除從圖中直接讀出近似值外，一般常用雙倒數法來求其精確值。此法是將式(2)的兩邊取倒數，以1/ r與1/ S來作圖，可求出 rmax和 Km值。

酶的抑制作用 酶的抑制作用是由於某些物質與酶相互作用后導致酶反應速率的下降。引起抑制作用的物質稱抑製劑。抑制作用有可逆與不可逆的。可逆抑制又有競爭性抑制、非競爭性抑制和反競爭性抑制之分。常用反應式(4)和式(5)來表示可能發生的相互作用。

E+IE=I　(4)

ES+I=ESI　(5)

此外I為抑製劑；EI為酶-抑製劑絡合物；ESI為酶-抑製劑-底物絡合物。抑製劑可以按式(4)和式(5)所示的相互作用，降低式(1)的反應速率。

①競爭性抑制作用　抑製劑與底物結構相似，與底物對酶分子上相同的活性部位發生競爭性結合，生成絡合物，如式(4)所示。競爭性抑制可用增加酶反應中底物濃度而逆轉以解除抑制作用。如果抑製劑是產物時，則稱競爭性產物抑制，反應過程中常採取增加底物濃度，或不斷將產物分離出去，降低產物濃度，提高反應速率。

②非競爭性抑制作用　是由於一種抑製劑既與酶也與酶-底物絡合物相互作用引起的結果。如式（4）和式(5)所示，這類抑制作用不能用提高底物濃度來消除。如果抑製劑是產物時，則稱為非競爭性產物抑制，在所有範圍的底物濃度下，產生的抑制作用是一致的。凡是有產物抑制的酶反應常優先採用連續管式或分批釜式反應器。

③反競爭性抑制作用　如式 (5)所示，抑製劑只與酶-底物絡合物相互作用。在低底物濃度下，其抑制作用比在高底物濃度下所產生的效應（對照百分率）要小。在不少酶反應過程中，底物也是抑製劑，底物抑制的酶反應常採用連續釜式反應器生產，它比分批式反應器有利。

以上三種可逆抑制酶反應的修正米氏方程式（見表），有一般表達式和典型表達式。前者用 K抑制常數；後者用 K, KP分別為底物和產物抑制常數; I表示抑製劑的濃度; P表示產物濃度。

酶動力學

溫度的影響 酶對溫度極為敏感，絕大多數酶在60℃以上即變性、失活。在低溫時酶反應進行緩慢；當溫度逐漸升高時，反應速率也逐漸升高；到最高峰時，溫度如繼續升高反應速率很快降低。

一種酶在一定條件下，只能在某一溫度時才表現出最大活力，這個溫度就是這種酶反應的最適溫度。各種酶都有它的最適溫度。最適溫度的出現，是由於溫度對酶的反應有雙重影響的結果。一方面同一般化學反應一樣，隨著溫度升高酶催化的反應速率也加快；另一方面是由於酶是蛋白質，隨著溫度升高會加速酶蛋白的變性，使酶的活性喪失。

pH的影響 反應介質的氫離子濃度也相當大地影響酶的活力。酶常常在某一pH範圍內才表現出最大活力，這種表現出酶最大活力時的pH，就是酶的最適pH。在最適pH範圍內，酶反應速率最大，否則酶反應速率就降低。

pH對酶反應速率的影響，一方面是由於酶本身是蛋白質，過酸或過鹼易使酶變性失活；另一方面主要是影響了酶分子的活性中心上有關基團的解離或底物的解離，影響酶與底物的結合，從而影響酶的活力。不同酶的最適pH可分佈在很廣的範圍內，從大約pH為2的蛋白酶到大約pH為10的精氨酸酶。某些酶可以跨越幾個pH單位的廣闊的最適pH範圍，而其他一些酶則有非常窄的最適pH。與最適溫度一樣，一種酶的最適pH可以隨所用的底物及其他實驗條件而變化。

米氏方程是基於質量作用定律而確立的，而該定律則基於自由擴散和熱動力學驅動的碰撞這些假定。然而，由於酶/底物/產物的高濃度和相分離或者一維/二維分子運動，許多生化或細胞進程明顯偏離質量作用定律的假定。在這些情況下，可以應用分形米氏方程。