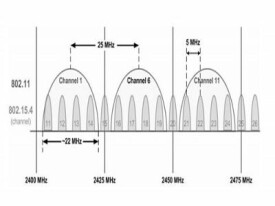
通道帶寬

模擬通道的帶寬 W=f2-f1 其中f1是通道能夠通過的最低頻率，f2是通道能夠通過的最高頻率，兩者都是由通道的物理特性決定的。當組成通道的電路製成了，通道的帶寬就決定了。為了使信號的傳輸的失真小些，通道要有足夠的帶寬。

數字通道是一種離散通道，它只能傳送離散值的數字信號，通道的帶寬決定了通道中能不失真的傳輸脈序列的最高速率。

一個數字脈衝稱為一個碼元，我們用碼元速率表示單位時間內信號波形的變換次數，即單位時間內通過通道傳輸的碼元個數。若信號碼元寬度為T秒，則碼元速率B=1/T。碼元速率的單位叫波特(Baud)，所以碼元速率也叫波特率。早在1924年，貝爾實驗室的研究員亨利·尼奎斯特就推導出了有限帶寬無雜訊通道的極限波特率，稱為尼奎斯特定理。若通道帶寬為W，則尼奎斯特定理指出最大碼元速率為B=2W(Baud)尼奎斯特定理指定的通道容量也叫尼奎斯特極限，這是由通道的物理特性決定的。超過尼奎斯特極限傳送脈衝信號是不可能的，所以要進一步提高波特率必須改善通道帶寬。

碼元攜帶的信息量由碼元取的離散值個數決定。若碼元取兩種離散值，則一個碼元攜帶1比特(bit)信息。若碼元可取四種離散值，則一個碼元攜帶2比特信息。即一個碼元攜帶的信息量n(bit)與碼元的種類數N有如下關係:n=log2N

單位時間內在通道上傳送的信息量(比特數)稱為數據速率。在一定的波特率下提高速率的途徑是用一個碼元表示更多的比特數。如果把兩比特編碼為一個碼元，則數據速率可成倍提高。

對此，我們有公式:

R=B log2N=2W log2N(b/s)

其中R表示數據速率，單位是每秒比特，簡寫為bps或b/s

數據速率和波特率是兩個不同的概念。僅當碼元取兩個離散值時兩者才相等。對於普通電話線路，帶寬為3000HZ，最高波特率為6000Baud。而最高數據速率可隨編碼方式的不同而取不同的值。這些都是在無雜訊的理想情況下的極限值。實際通道會受到各種雜訊的干擾，因而遠遠達不到按尼奎斯特定理計算出的數據傳送速率。香農(shannon)的研究表明，有雜訊的極限數據速率可由下面的公式計算：

C =W log2（1+s/n）

這個公式叫做香農定理，其中W為通道帶寬，S為信號的平均功率，N為雜訊的平均功率，s/n叫做信噪比。由於在實際使用中S與N的比值太大，故常取其分貝數(db)。分貝與信噪比的關係為 : db=10lgs/n

例如當s/n為1000，信噪比為30db。這個公式與信號取的離散值無關，也就是說無論用什麼方式調製，只要給定了信噪比，則單位時間內最大的信息傳輸量就確定了。例如通道帶寬為3000HZ，信噪比為30db，則最大數據速率為

C=3000log2（1+1000）≈3000×9.97≈30000b/s

這是極限值，只有理論上的意義。實際上在3000HZ帶寬的電話線上數據速率能達到9600b/s就很不錯了。

綜上所述，我們有兩種帶寬的概念，在模擬通道，帶寬按照公式W=f2-f1 計算，例如CATV電纜的帶寬為600HZ或1000HZ；數字通道的帶寬為通道能夠達到的最大數據速率，例如乙太網的帶寬為10MB/S或100MB/S，兩者可通過香農定理互相轉換。

通道帶寬

頻段帶寬是發送無線信號頻率的標準。在常用的2.4-2.4835GHz頻段上，每個通道的頻段帶寬為20MHz；前者工作的協議有b/g/n，後者有ac/a/n。

頻率越高越容易失真，其中20MHz在11n的情況下能達到144Mbps（怎麼計算的？）帶寬，它穿透性較好，傳輸距離遠（約100米左右）；40MHz在11n的情況下能達到300Mbps帶寬，穿透性稍差，傳輸距離近（約50米左右）。

信號帶寬

信號帶寬是指在自由空間（包括空氣和真空）傳播的射頻頻段的電磁波。

電磁波包含很多種類，按照頻率從低到高的順序排列為：無線電波、紅外線、可見光、紫外線、X射線及γ射線。無線電波分佈在3Hz到3000GHz的頻率範圍之間。在這個頻譜內可以細劃為12個波段頻率越低，傳播損耗越小，覆蓋距離越遠，繞射能力也越強。但是低頻段的頻率資源緊張，系統容量有限，因此低頻段的無線電波主要應用於廣播、電視、尋呼等系統。

高頻段頻率資源豐富，系統容量大。但是頻率越高，傳播損耗越大，覆蓋距離越近，繞射能力越弱。另外，頻率越高，技術難度也越大，系統的成本相應提高。