共找到2條詞條名為臨界值的結果 展開
- 臨界值
- 闕值
臨界值
臨界值
臨界值是指物體從一種物理狀態轉變到另外一種物理狀態時,某一物理量所要滿足的條件,相當於數學中常說的駐點。因此利用臨界狀態求解物理量的最大值與最小值,就成了物理中求解最值的一種重要的方法。有人認為利用臨界狀態求解最值應謹慎,首先須分清兩狀態之間的關係。
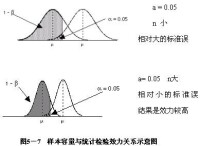
臨界值
1.兩狀態同時存在且最值在臨界點取得
例1如圖1所示,質量為m的小球以初速度v0從A點開始沿光滑圓形軌道槽上滑,求小球能通過最高點B做圓周運動的最小初速度v0.
分析由於軌道槽光滑,整個過程系統機械能守恆。小球在A點的總能為。
Ek=(1/2)mv02,
在B點的總能量為
E=(1/2)mv02+2mgR,
則(1/2)mv02=(1/2)mvB2+2mgR,
顯然在①式中要使v0最小,則要求vB最小,因此求v0的最小值便轉化為求vB的最小值.但僅根據①式我們還不能確定vB的最小值.要確定vB的最小值還要考慮題中所提供的條件:小球能通過B點做圓周運動而不下落與下落之間存在著臨界速度,即vB必須大於或等於這個臨界速度,小球才不會下落。因此臨界速度就是小球經過B點而不下落的最小速度,從而把求解小球初速度的最小值轉化為求小球沿豎直圓形軌道做圓周運動的臨界速度。
解小球做圓周運動達到最高點B時的受力情況是:受重力mg和軌道對其的壓力N作用,兩者的合力為小球提供做圓周運動的向心力,即
F心=mg+N,所以(mvB2/R)=mg+N,把②式代入①式可得
結論對於這類最值問題,由於最值在臨界點取得,我們可以利用臨界值與最值兩者之間的關係,根據物體在某一變化過程中在臨界點所遵循的物理規律找出其臨界值,從而求出最值.這對用其他一些方法求解時顯得複雜或根本求不出最值的問題,不能說不是一條捷徑。
2.兩狀態同時存在,但最值不在臨界點取得
所示,一質量為10kg的物體,受到一水平向左的恆力F=10N作用,而從A點開始以初速度v0=10m/s向右沿光滑水平面滑動,求在8s鍾內物體的最大位移(以向右為正)。分析顯然該題中速度存在著一個臨界點,即v=0的點.根據公式vt2-v02=2as可得s臨=50m.但應注意到v=0所需要的時間是10s,當時間小於10s時,位移s為增函數,即smax=10×8-(1/2)×1×82=48m,所以s臨≠smax.結論對於這類最值問題,由於最值不在臨界點取得,不能把臨界值當成最值,但可以根據題中條件藉助於臨界值確定出最值。
3.存在臨界點不存在最值,但變化量無限趨向臨界值
例3如所示,位於水平面的兩條平行導軌,間距為L,電源電動勢為E,所有電阻為R,金屬棒ab質量為m,它與導軌間的摩擦因數為μ.整個迴路處在磁感強度為B的均勻磁場中.當開關S閉合后,ab棒由靜止開始向右滑動.問ab棒的速度是否能達到最大值?如能達到,求出其最大值。
分析這是一道非常經典的電磁學與力學的綜合題,一般的解法都這樣認為:由於ab棒開始是做加速度逐漸減小的運動,因此認為當加速度變為0時速度達到最大,即速度在其臨界點達到最大值,從而利用下式求出速度的最大值
mgμ=BIL,
mgμ=BL(E-BLv/R),
max=(E/BL)-(mgμR/B2L2).
下面,我們再根據棒ab在整個變化過程中所遵循的物理規律,用數學方法求出棒ab的速度隨時間變化的表達式,然後再討論其最值,由於是變力,因此我們必須列出其遵循的微分方程,即
a=(dv/dt)=(BLI-f/m),③
I=(E′/R)=(E-BLv/R), ④
把④代入③可得
(dv/dt)+(B2L2/mR)v=(BL/mR)-gμ,⑤
⑤式是一階線性微分方程,其通解為
⑥當t=0時,v=0,代入⑥式可得
C=-(BLE-gμmR)/(B2L2),
所以討論顯然v是單調遞增函數,無限趨向於其臨界值:(E/BL)-(mgμR/B2L2),所以沒有最大值.只有t→∞時,v才能取極限值(臨界值),也就是常說的收尾速度。
結論諸如此類的題目例子很多,如電容器充放電時電容器上的電壓,雨點受到阻力為f=-kv的速度等,筆者曾研究過它們的運動規律都有一個共同特點:即所求變化的物理量都是聯鎖反饋性變化且遵循一階線性微分方程.由於存在臨界點且容易確定,往往會錯誤的把它當成最值,而實際上並不存在最值,只能在近似的情況下認為其存在最值且等於其臨界值。
綜上所述,筆者認為臨界點是由物理規律所決定的一種狀態,它可以由滿足該狀態的物理規律來確定,是客觀存在的.而最值的求解,嚴格地講,應是在一定條件和物理規律支配下的一個變化過程,此過程能不能實現,最值是否在臨界點取得,要綜合分析其所滿足的條件和所遵循的物理規律,把握好物理量的變化特徵,同時還要遵循一定的數學原理.在某些情況下(如例1),臨界值和最值相當,我們可以通過臨界點求最值,從而獲得事半功倍的效果.而在另外一些情況下(如例2和例3),最值與臨界值之間沒有必然聯繫.因此,在最值的求解過程中,我們只能把尋找臨界點作為求最值的一種方法,而不能把它與最值的求解同等起來.
