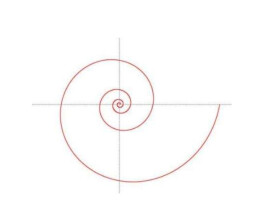
阿基米德螺線
亦稱“等速螺線”
阿基米德螺線(阿基米德曲線),亦稱“等速螺線”。當一點P沿動射線OP以等速率運動的同時,該射線又以等角速度繞點O旋轉,點P的軌跡稱為“阿基米德螺線”。其首次由阿基米德在著作《論螺線》中給出了定義。稍遲於阿基米德的阿波羅尼斯用圓柱螺線解決了化圓為方問題。
極坐標方程式
阿基米德螺線
笛卡爾坐標方程式為:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t *360)
z=0
阿基米德螺旋線的標準極坐標方程: r(θ)= a+ b(θ)
式中:
b-阿基米德螺旋線係數,mm/°,表示每旋轉1度時極徑的增加(或減小)量;
θ-極角,單位為度,表示阿基米德螺旋線轉過的總度數;
a-當θ=0°時的極徑,mm。
改變參數a將改變螺線形狀,b控制螺線間距離,通常其為常量。阿基米德螺線有兩條螺線,一條θ>0,另一條θ<0。兩條螺線在極點處平滑地連接。把其中一條翻轉 90°/270°得到其鏡像,就是另一條螺線。
在極坐標系與平面直角坐標系(笛卡爾坐標系)間轉換:
圖一
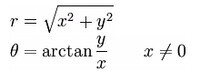
圖二
極坐標系中的兩個坐標 r 和 θ 可以由下面的公式轉換為直角坐標系下的坐標值(圖一) 。由上述二公式,可得到從直角坐標系中x 和 y 兩坐標如何計算出極坐標下的坐標(圖二)。
在x=0的情況下:若y為正數,則θ=90°(π/2radians);若y為負,則θ=270°(3π/2radians).

阿基米德螺線
還有舉重滑輪、灌地機、揚水機以及軍事上用的拋石機等。被稱作“阿基米德螺旋”的揚水機至今仍在埃及等地使用。
一些噴淋冷卻塔所用的螺旋噴嘴噴出噴淋液的運動軌跡也為阿基米德螺線。
更多曲線參見曲線列表
阿基米德(約公元前287~前212),古希臘偉大的數學家、力學家。他公元前287年生於希臘敘拉古附近的一個小村莊。11歲時去埃及,到當時世界著名學術中心、被譽為“智慧之都”的亞歷山大城跟隨歐幾里得的學生柯農學習,以後和亞歷山大的學者保持緊密聯繫,因此他算是亞歷山大學派的成員。
公元前240年,阿基米德由埃及回到故鄉敘拉古,並擔任了國王的顧問。從此開始了對科學的全面探索,在物理學、數學等領域取得了舉世矚目的成果,成為古希臘最偉大的科學家之一。後人對阿基米德給以極高的評價,常把他和牛頓、高斯並列為有史以來三個貢獻最大的數學家。
據說,阿基米德螺線最初是由阿基米德的老師柯農(歐幾里德的弟子)發現的。柯農死後,阿基米德繼續研究,又發現許多重要性質,因而這種螺線就以阿基米德的名字命名了。
1.阿基米德螺線的幾何畫法
以適當長度(OA)為半徑,畫一圓O;作一射線OA;作一點P於射線OA上;模擬點A沿圓O移動,點P沿射線OA移動;畫出點P的軌跡;隱藏圓O、射線OA&點P;即可得到螺線
2.阿基米德螺線的簡單畫法
有一種最簡單的方法畫出阿基米德螺線,用一根線纏在一個線軸上,在其遊離端綁上一小環,把線軸按在一張紙上,並在小環內套一支鉛筆,用鉛筆拉緊線,並保持線在拉緊狀態,然後在紙上畫出由線軸鬆開的線的軌跡,就得到了阿基米德螺線。
螺線之所以在生命體中廣泛存在,是由於螺線的若干優良性質所確定。而這些優良性質直接或間接地使生命體在生存鬥爭中獲得最佳效果。由於在柱面內過柱面上兩點的各種曲線中螺線長度最短,對於蔦蘿、紫藤、牽牛花等攀緣植物而言,如何用最少的材料、最低的能耗,使其莖或藤延伸到光照充足的地方是至關重要的。而在各種曲線中,螺線就起到省材、節約能量消耗的作用,在相同的空間中使其葉子獲取較多的陽光,這對植物光合作用尤為重要,像煙草等植物輪狀葉序就是利用形成的螺旋面能在狹小的空間中(其他植物的夾縫中)獲得最大的光照面積,以利於光合作用。形成螺線狀的某些物體還有一種物理性質,即像彈簧一樣具有彈性(或伸縮性)。在植物中絲瓜、葫蘆等莖上的擬圓柱螺線狀的觸鬚利用這個性質,能使其牢固地附著其他植物或物體上。即使有外力或風的作用,由於螺線狀觸鬚的伸縮性,使得纖細的觸鬚不易被拉斷,並且當外力(或風)消失后,保證其莖葉又能恢復到原來的位置。螺旋線對於生活在水中的大多數螺類軟體動物也是十分有意義的。觀察螺類在水中的運動方式,通常是背負著外殼前進,殼體直徑粗大的部分在前,螺尖在後。當水流方向與運動方向相反時,水流沿著殼體螺線由直徑大的部分旋轉到直徑小的部分直到螺尖。水速將大大減小,這樣位於殼體后水的靜壓力將大於殼體前端的靜壓力。在前後壓力差的作用下,殼體將會自動向前運動。這樣一來,來自水流的阻力經錐狀螺線的轉化變為前進的動力。除此而外,分佈在螺類外殼上的螺線像一條肋筋,大大增加了殼體的強度,也分散了作用在殼體上的水壓。
阿基米德螺線,亦稱“等速螺線”。當一點P沿動射線OP一等速率運動的同時,這射線有以等角速度繞點O旋轉,點P的軌跡稱為“阿基米德螺線”。
它的極坐標方程為:r = aθ
這種螺線的每條臂的距離永遠相等於 2πa。
笛卡爾坐標
方程式為:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t * 360)
z=0
一動點沿一直線作等速移動的同時,該直線又繞線上一點O作等角速度旋轉時,動點所走的軌跡就是阿基米德渦線。直線旋轉一周時,動點在直線上移動的距離稱為導程用字母S表示。
阿基米德渦線在凸輪設計、車床卡盤設計、渦旋彈簧、螺紋、蝸桿設計中應用較多。阿基米德渦線畫法如圖:
(1)先以導程S為半徑畫圓,再將圓周及半徑分成相同的n等分,圖中n=8;
(2)以O為圓心,作各同心圓弧於相應數字的半徑相交,得交點Ⅰ、Ⅱ、Ⅲ、…Ⅷ各點,即為阿基米德渦線上的點;
(3)依次光滑連接各點,即得阿基米德渦線。
與希皮亞斯割圓曲線相類似,阿基米德螺線不但可以用來三等分角,也可以用來化圓為方。不過,後者也是阿基米德自己完成的。如圖一,螺線P=aθ的極點為O,第一圈終於點A。以O為圓心,a為半徑作圓,則圓周長等於=OA。這樣,阿基米德輕易解決化圓為方問題。
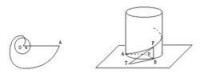
圖一
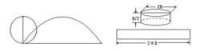
圖二
文藝復興時期,義大利著名藝術大師達·芬奇(1452~1519)為化圓為方問題所吸引,並獲巧妙方法。如圖4-2-29,設圓半徑為R,以圓為底作高為R/2的圓柱,然後將圓柱在平面上滾動一周,得矩形。將矩形化方,即完成化圓為方。
以上我們看到,希臘人很早就意識到(但未能證明)三大難題不能以尺規在有限步驟內完成。但它們看似如此簡單,以至希臘人未能抵制誘惑;他們不斷尋求尺規以外的方法,結果導致圓錐曲線、割圓曲線、蚌線、蔓葉線和螺線等高次曲線和超越曲線的相繼發現。三大難題使一代又一代希臘數學家顯示了非凡的聰明才智,並深刻影響了希臘幾何的整個發展過程。
三大難題的魅力並未隨希臘文明的淪亡而消失。事實上,從希臘以後特別是歐洲文藝復興時期以來直到本世紀,對於它們的研究從未停止過。
1837年,年輕的法國數學家萬采爾(P. L. Wantzel,1814~1848)證明了三等分角和倍立方尺規作圖之不可能性。1882年,德國數學家林德曼(C. Lindemann, 1852~1938)證明了π的超越性,從而證明了化圓為方的尺規作圖之不可能性。以後數學家們又還建立了兩條一般定理:
定理1 任何可用尺規由已知單位長度作出的量必為代數數;
定理2 若一有理係數三次方程沒有有理根,則它的根不可能用尺規由一給定單位長度作出。