全等形
能夠完全重合的圖形
全等形在通常的平面幾何里,把平面上的一個圖形搬到另一個圖形上,如果它們完全重合,那麼這兩個圖形叫做全等圖形,簡稱全等形。
一個圖形經過平移、翻折、旋轉后,位置變化了,但形狀和大小都沒有改變,即平移、翻折、旋轉前後的圖形全等。即一個圖形經過平移、旋轉或翻折等變換后,所得到的新圖形一定與原圖形全等。反過來,兩個全等的圖形經過平移、旋轉或翻折變換后一定可以重合。
全等形的特點是形狀、大小相同。
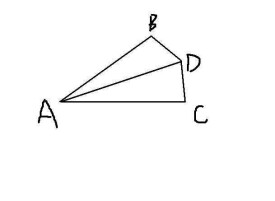
例1:圖1中的圖形的形狀、大小相同,即為全等形。

圖1
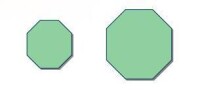
圖2
例2:圖2中的圖形的形狀相同,大小不同,不是全等形。
例3:圖3中的圖形的大小相同,形狀不同,不是全等形。
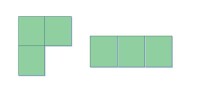
圖3
相似形:形狀相同的平面圖形。特點是形狀形同,大小不一定相同。
全等形:能夠完全重合的平面圖形。特點是形狀、大小相同。
全等形在數學中被廣泛應用。其中應用較多的是全等三角形。全等三角形是指能夠完全重合的三角形。
全等三角形的性質:
1.全等三角形對應邊相等;
2.全等三角形對應角相等。
判定定理:
1.三邊對應相等的兩個三角形全等(簡稱SSS或“邊邊邊”);
2.兩邊和它們的夾角對應相等的兩個三角形全等(簡稱SAS或“邊角邊”);
3.兩角和它們的夾邊對應相等的兩個三角形全等(簡稱ASA或“角邊角”);
4.兩個角和其中一個角的對邊對應相等的兩個三角形全等(簡稱AAS或“角角邊”);
5.直角三角形全等條件是斜邊及一直角邊對應相等的兩個直角三角形全等(簡稱HL或“斜邊,直角邊”)。
在三角形全等的判定中,沒有 AAA(角角角)和 SSA(邊邊角),其中 A是英文角的縮寫(angle), S是英文邊的縮寫(side)。H是英文斜邊的縮寫(hypotenuse),L是英文直角邊的縮寫(leg)。
全等形
全等形
例1.已知圖4中,與為全等三角形,,求DE長度。
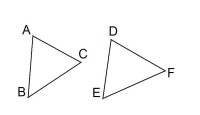
圖4
例2.將一個正方形分成4個全等的三角形,列舉2種分割方法即可。
解:如圖5所示。
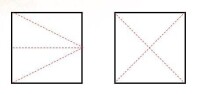
圖5