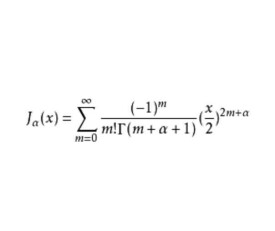第一類貝塞爾函數
第一類貝塞爾函數
第一類貝塞爾函數(Bessel function of the first kind),常簡稱貝塞爾函數,為貝塞爾方程的第一解。貝塞爾函數的具體形式隨方程中任意實數或複數α變化而變化(相應地,α被稱為其對應貝塞爾函數的階數)。實際應用中最常見的情形為α是整數n,對應解稱為n 階貝塞爾函數。
貝塞爾函數的幾個正整數階特例早在18世紀中葉就由瑞士數學家丹尼爾·伯努利在研究懸鏈振動時提出了,當時引起了數學界的興趣。丹尼爾的叔叔雅各布·伯努利,歐拉、拉格朗日等數學大師對貝塞爾函數的研究作出過重要貢獻。1817年,德國數學家貝塞爾在研究開普勒提出的三體引力系統的運動問題時,第一次系統地提出了貝塞爾函數的總體理論框架,後人以他的名字來命名了這種函數。
貝塞爾方程是在圓柱坐標或球坐標下使用分離變數法求解拉普拉斯方程和亥姆霍茲方程時得到的(在圓柱域問題中得到的是整階形式;在球形域問題中得到的是半奇數階形式,因此貝塞爾函數在波動問題以及各種涉及有勢場的問題中佔有非常重要的地位,最典型的問題有:
(1)在圓柱形波導中的電磁波傳播問題;
(2)圓柱體中的熱傳導問題;
(3)圓形(或環形)薄膜的振動模態分析問題;
在其他一些領域,貝塞爾函數也相當有用。譬如在信號處理中的調頻合成(FM synthesis)或凱澤窗(Kaiser window)的定義中,都要用到貝塞爾函數。
貝塞爾方程是一個二階常微分方程
必然存在兩個線性無關的解。針對各種具體情況,人們提出了表示這些解的不同形式。
第一類貝塞爾函數(Bessel function of the first kind)作為貝塞爾方程的第一解,又稱貝塞爾函數,有時會簡稱為函數,記作。
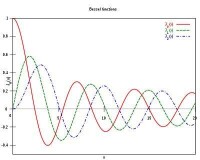
0階、1階和2階第一類貝塞爾函數(貝塞爾J函數)曲線
上式中為函數(它可視為階乘函數向非整型自變數的推廣)。第一類貝塞爾函數的形狀大致與按速率衰減的正弦或餘弦函數類似,但它們的零點並不是周期性的,另外隨著''x''的增加,零點的間隔會越來越接近周期性。右圖所示為階、階和階第一類貝塞爾函數。
如果α不為整數,則和線性無關,可以構成微分方程的一個解系。反之若α是整數,那麼上面兩個函數之間滿足如下關係:
於是兩函數之間已不滿足線性無關條件。為尋找在此情況下微分方程與線性無關的另一解,需要定義第二類貝塞爾函數。
α為整數時貝塞爾函數的另一種定義方法由下面的積分給出:
這個積分式就是貝塞爾當年提出的定義,而且他還從該定義中推出了函數的一些性質。另一種積分表達式為:
貝塞爾函數可以用超幾何級數表示成下面的形式:
為整數,由於函數線性相依的特性(用了一個,少了一個,所以要再弄出一個出來),才需定義Neumann函數(即第二類貝塞爾函數)。