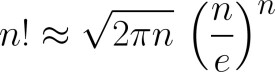斯特林公式
斯特林公式
斯特林公式(Stirling's approximation)是一條用來取n的階乘的近似值的數學公式。一般來說,當n很大的時候,n階乘的計算量十分大,所以斯特林公式十分好用,而且,即使在n很小的時候,斯特林公式的取值已經十分準確。
斯特林公式在理論和應用上都具有重要的價值,對於概率論的發展也有著重大的意義。在數學分析中,大多都是利用Г函數、級數和含參變數的積分等知識進行證明或推導,很為繁瑣冗長。近年來,一些國內外學者利用概率論中的指數分佈、泊松分佈、χ²分佈證之。
或更精確的
或
令
則
所以 即,即單調遞減,又由積分放縮法有
即,即
由單調有界定理 的極限存在,
設
利用Wallis公式,
所以
即
斯特林數判斷階乘位數
#include
#include
#include
#include
const double e = 2.71828182845;
const double pi = 3.1415926;
int main(void) {
int t, i, f, v;
double a, s;
const double log10_e = log10(e);
const double log10_2_pi = log10(2.0*pi)/2.0;
while (scanf("%d", &t) != EOF && t) {
for (i = 0; i < t; ++i) {
scanf("%d\n", &v);
if (1 == v) {printf("1\n"); continue;}
a = v;
s = log10_2_pi + (a+0.5)*log10(a) - a * log10_e;
f = ceil(s);
printf("%d\n", f); } }
return 0; }