牛頓插值法
牛頓插值法
插值法利用函數f(x)在某區間中若干點的函數值,作出適當的特定函數,在這些點上取已知值,在區間的其他點上用這特定函數的值作為函數f(x)的近似值。
牛頓插值法相對於拉格朗日插值法具有承襲性的優勢,即在增加額外的插值點時,可以利用之前的運算結果以降低運算量。
目錄
如果這特定函數是多項式,就稱它為插值多項式。利用插值基函數很容易得到拉格朗日插值多項式,公式結構緊湊,在理論分析中甚為方便,但當插值節點增減時全部插值基函數均要隨之變化,整個公式也將發生變化,這在實際計算中是很不方便的,為了克服這一缺點,提出了牛頓插值。
牛頓插值法的特點在於:每增加一個點,不會導致之前的重新計算,只需要算和新增點有關的就可以了。
假設已知n+1n+1個點相對多項式函數ff的值為:(x0,f(x0)),(x1,f(x1)),(x2,f(x2)),⋯,(xn,f(xn))(x0,f(x0)),(x1,f(x1)),(x2,f(x2)),⋯,(xn,f(xn)),求此多項式函數f。
先從求滿足兩個點(x0,f(x0)),(x1,f(x1))(x0,f(x0)),(x1,f(x1))的函數f1(x)f1(x)說起:
假設f1(x)=f(x0)+b1(x−x0)f1(x)=f(x0)+b1(x−x0),
現在我們增加一個點,(x0,f(x0)),(x1,f(x1)),(x2,f(x2))(x0,f(x0)),(x1,f(x1)),(x2,f(x2)),求滿足這三個點的函數f2(x)f2(x):
假設f2(x)=f1(x)+b2(x−x0)(x−x1)f2(x)=f1(x)+b2(x−x0)(x−x1),
以此類推,我們得到牛頓插值法為: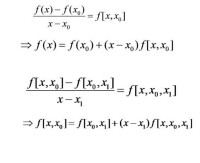
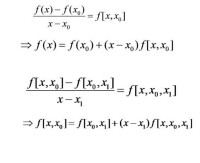
牛頓插值法