阿拉伯數字

阿拉伯數字由0，1，2，3，4，5，6，7，8，9共10個計數符號組成。採取位值法，高位在左，低位在右，從左往右書寫。藉助一些簡單的數學符號（小數點、負號、百分號等），這個系統可以明確的表示所有的有理數。為了表示極大或極小的數字，人們在阿拉伯數字的基礎上創造了科學記數法。

公元500年前後，隨著經濟、種姓制度的興起和發展，印度次大陸西北部的旁遮普地區的數學一直處於領先地位。天文學家阿葉彼海特在簡化數字方面有了新的突破：他把數字記在一個個格子里，如果第一格里有一個符號，比如是一個代表1的圓點，那麼第二格里的同樣圓點就表示十，而第三格里的圓點就代表一百。這樣，不僅是數字元號本身，而且是它們所在的位置次序也同樣擁有了重要意義。以後，印度的學者又引出了作為零的符號。可以這麼說，這些符號和表示方法是今天阿拉伯數字的老祖先了。

公元3世紀，古印度的一位科學家巴格達發明了阿拉伯數字。最古的計數目大概至多到3，為了要設想“4”這個數字，就必須把2和2加起來，5是2加2加1，3這個數字是2加1得來的，大概較晚才出現了用手寫的五指表示5這個數字和用雙手的十指表示10這個數字。這個原則實際也是數學計算的基礎。羅馬的計數只有到Ⅴ（即5）的數字，Ⅹ（即10）以內的數字則由Ⅴ（5）和其它數字組合起來。Ⅹ是兩個Ⅴ的組合，同一數字元號根據它與其他數字元號位置關係而具有不同的量。這樣就開始有了數字位置的概念，在數學上這個重要的貢獻應歸於兩河流域的古代居民，後來古鯿人在這個基礎上加以改進，併發明了表達數字的1，2，3，4，5，6，7，8，9，0十個符號，這就成為今天記數的基礎。八世紀印度出現了有零的符號的最老的刻版記錄。當時稱零為首那。

兩百年後，團結在伊斯蘭教下的阿拉伯人征服了周圍的民族，建立了東起印度，西從非洲到西班牙的阿拉伯帝國。後來，這個伊斯蘭大帝國分裂成東、西兩個國家。由於這兩個國家的各代君王都獎勵文化和藝術，所以兩國的首都都非常繁榮，而其中特別繁華的是東都——巴格達，西來的希臘文化，東來的印度文化都彙集到這裡來了。阿拉伯人將兩種文化理解消化，從而創造了獨特的阿拉伯文化。

大約700年前後，阿拉伯人征服了旁遮普地區，他們吃驚地發現：被征服地區的數學比他們先進。於是設法吸收這些數字。

771年，印度北部的數學家被抓到了阿拉伯的巴格達，被迫給當地人傳授新的數學符號和體系，以及印度式的計算方法（用的計演演算法）。由於印度數字和印度計數法既簡單又方便，其優點遠遠超過了其他的計演演算法，阿拉伯的學者們很願意學習這些先進知識，商人們也樂於採用這種方法去做生意。

後來，阿拉伯人把這種數字傳入西班牙。公元10世紀，又由教皇熱爾貝·奧里亞克傳到歐洲其他國家。公元1200年左右，歐洲的學者正式採用了這些符號和體系。至13世紀，在義大利比薩的數學家費婆拿契的倡導下，普通歐洲人也開始採用阿拉伯數字，15世紀時這種現象已相當普遍。那時的阿拉伯數字的形狀與現代的阿拉伯數字尚不完全相同，只是比較接近而已，為使它們變成今天的1、2、3、4、5、6、7、8、9、0的書寫方式，又有許多數學家花費了不少心血。

阿拉伯數字起源於印度，但卻是經由阿拉伯人傳向四方的，這就是後來人們誤解阿拉伯數字是阿拉伯人發明的原因。

瓜廖爾石碑876年

印度數碼中表示零的“點號”逐漸演變為圓，也就是現在的“0”這一演變過程最遲完成於九世紀。印度876年出土的瓜廖爾石碑見證這一過程。該石碑上有記載無誤的“0”，用圓圈表示零，是數學史的一大發明。“0”的出現是數學史上一大創造。“0”一直被人們稱為阿拉伯數字，其實，它的誕生地卻是在古代印度，它的起源深受佛教大乘空宗的影響。大乘空宗流行於公元三至六世紀的古代印度。恰正是在它流行後期，在印度產生了新的整數的十進位值制記數法，規定出十個數字的符號。以前計算到十數時空位加一點。用“.”表示，這時發明了“0”來代替。“0”的梵文名稱為Sunya，漢語音譯為“舜若”，意譯為“空”。0乘以任何一個數，都使這個數變成0。大乘空宗由印度龍樹及其弟子提婆所創立，強調“一切皆空”。0的這一特殊就反映了“一切皆空”這一命題所留下的痕迹。0是正數和負數的分界點，也是解析幾何中笛卡兒坐標軸上的原點。沒有0也就沒有原點，也就沒有了坐標系，幾何學大廈就會分崩離析。這種認識，同樣有可能受了大乘空宗的啟發。大乘空宗的“空”，在某種意義上也可以看做是原點，是佛教認識萬事萬物的根本出發點。大乘空宗認為，無論是正面的天堂還是反面的地獄，不管是天神或是魔鬼，都不免入相，脫離不了輪迴之苦。天神享盡福報，照樣會墮入畜生道或餓鬼道，也有可能走向自己對立面而成為魔。大乘佛教說“空”道“有”，都強調不可執著。這種說法與0的特殊在數學上表述，在哲學上有其相同之處。公元七世紀中葉，印度的記數法開始向西方傳播，公元八世紀末傳入阿拉伯國家。印度數字經阿拉伯人改進後傳入歐洲，被稱為阿拉伯數字或印度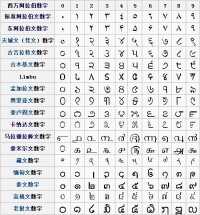——阿拉伯數字。

公元前2500年前後，古印度出現了一種稱為哈拉巴數碼的銘文記數法。到公元前後通行起兩種數碼：卡羅什奇數字和婆羅門數字。公元3世紀，印度科學家巴格達發明了阿拉伯數字。公元4世紀后阿拉伯數字中零的符號日益明確，使記數逐漸發展成十進位值制，例如公元8世紀后出現的德溫那格利數字。

大約公元9世紀，印度數字傳入阿拉伯地區，從原來的婆羅門數字導出兩種阿拉伯數字：被中東的阿拉伯人使用的東阿拉伯數字和被西班牙的阿拉伯人使用的西阿拉伯數字。東阿拉伯數字和阿拉伯人使用的形式很相似，西阿拉伯數字後來發展成我們廣泛使用的形式。

阿拉伯數字筆畫簡單，書寫方便，加上使用十進位制便於運算，逐漸在各國流行起來，成為世界各國通用的數字。

阿拉伯數字在Unicode碼中的位置是048到057。

十個數字元號後來由阿拉伯人傳入歐洲，被歐洲人誤稱為阿拉伯數字。由於採用計數的十進位法，加上阿拉伯數字本身筆畫簡單，寫起來方便，看起來清楚，特別是用來筆算時，演算很便利。因此隨著歷史的發展，阿拉伯數字逐漸在各國流行起來，成為世界各國通用的數字。

阿拉伯數字傳入我國，大約是13到14世紀。由於我國古代有一種數字叫“算籌”，寫起來比較方便，所以阿拉伯數字當時在我國沒有得到及時的推廣運用。20世紀初，隨著我國對外國數學成就的吸收和引進，阿拉伯數字在我國才開始慢慢使用，阿拉伯數字在我國推廣使用才有100多年的歷史。阿拉伯數字現在已成為人們學習、生活和交往中最常用的數字了。

阿拉伯數字容易通過改變小數點位置而產生變化。所以在特殊場合（如銀行）不能完全替代大寫的漢字。

在科技書刊中，阿拉伯數字因其“筆畫簡單、結構科學、形象清晰、組數簡短”等特點，有著很高的使用頻率，其用法是否正確及規範，直接關係到科技期刊的質量。

阿拉伯數字使用的場合

科技書刊阿拉伯數字使用的總體原則是：凡是可以使用阿拉伯數字，且又很得體的地方，均應使用阿拉伯數字。主要使用場合有：

（1）物理量量值。物理量量值必須使用阿拉伯數字，且數字后的計量單位必須使用我國法定計量單位，如：3 kg、45 m、2 min 等。

（2）公元世紀、年代、年、月、日、時刻。如：20 世紀 90 年代、2005 年 12 月 12 日、16時 15 分等。

（3）計數單位前的數字。計數單位前大於 10 的數字必須使用阿拉伯數字，整數 1~10，凡是可以使用阿拉伯數字，且又很得體的地方，也應該用阿拉伯數字。如：12 支鉛筆、4 根管子、1 朵花等。

（4）計數的數字。不論是圖表還是記述性文字中，計數的數字都必須用阿拉伯數字，包括整數、小數、百分數、比例等。

（5）型號、編號、序號、代號等。科技論文中經常出現儀器型號、樣品編號、標準號等，這些都應使用阿拉伯數字，序數詞前經常帶有“第”字。如：ML 1332 檢測儀、GB 18745、第8 小組等。

2. 阿拉伯數字書寫規則

（1）純小數小數點前的“0”不能省略。不論是敘述性文字或圖表中，純小數小數點前的“0”都不能省略，不能出現諸如“.27、.39”等格式的數字。

（2）阿拉伯數字不能與除“萬”、“億”及 SI 詞頭中文符號外的漢字數詞連用。如：“一千三百萬”可以改寫成“1 300 萬”，但不能寫成“1 千 3 百萬”。

（3）4 位或 4 位以上的數字，在書寫時採用三位分節法。