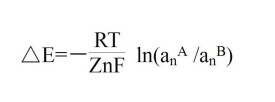能斯特方程
能斯特方程
能斯特方程(Nernst)是用以定量描述離子ri在A、B兩體系間形成的擴散電位的方程表達式。在電化學中,能斯特方程用來計算電極上相對於標準電勢(E0)來說的指定氧化還原對的平衡電壓(E)。能斯特方程只能在氧化還原對中兩種物質同時存在時才有意義。
E=E(標準)-(RT)/(nF)ln([Zn]/[Cu])
對於任一電池反應:
aA+bB=cC+dD
E=E(標準)-(RT)/(nF)ln(([C]·[D])/([A]·[B]))……………………⑴
⑴這個方程就叫做能斯特(Nernst,W.H.1864~1941)方程。它指出了電池的電動勢與電池本性(E)和電解質濃度之間的定量關係。
當溫度為298K時,能斯特方程為:
E=E(標準)-(0.0257/n)lg(([C]·[D])/([A]·[B]))……………………⑵
當溫度為298K時,Cu-Zn原電池反應的能斯特方程為:
E=E(標準)-(0.0592/n)lg([Zn]/[Cu])……………………⑶
該方程的圖形應為一直線,其截距為E=1.10V,斜率為-0.0592/2=-0.03,與前述實驗結果一致。將⑶式展開,可以求到某電極的能斯特方程:
E=φ(+)-φ(-)=[φ(標準,+)-φ(標準,-)]-(0.0592/2)lg([Zn]/[Cu])
={φ(標準,+)+(0.0592/2)lg[Cu]}-{φ(標準,-)+(0.0592/2)lg[Zn]}
所以φ(+)=φ(標準,+)+(0.0592/2)lg[Cu]
φ(-)=φ(標準,-)+(0.0592/2)lg[Zn]
歸納成一般的通式:
φ=φ(標準)+(0.0592/n)lg([氧化型]/[還原型])……………………⑷
式中n——電極反應中電子轉移數。
[氧化型]/[還原型]——表示參與電極反應所有物質濃度的乘積與反應產物濃度乘積之比。而且濃度的方次應等於他們在電極反應中的係數。
純固體、純液體的濃度為常數,作1處理。離子濃度單位用mol/L(嚴格地應該用活度)。氣體用分壓表示。

能斯特方程中的參數
MnO2+4HCl=MnCl2+Cl2+2H2O
還原劑的電極反應:
Cl2+2e-=2Cl-φ(標準)=1.3583V
氧化劑的電極反應:
MnO2+4H++2e-=Mn2++2H2Oφ(標準)=1.228V
E(標準)=1.228-1.3583=-0.1523<0
所以反應不能自發地向右進行。
用φ(標準)判斷結果與實際反應方向發生矛盾的原因在於:鹽酸不是1mol/L,Cl2分壓也不一定是101.3kpa,加熱也會改變電極電勢的數值。由於化學反應經常在非標準狀態下進行,這就要求研究離子濃度、溫度等因素對電極電勢的影響。
但是由於反應通常皆在室溫下進行,而溫度對電極電勢的影響又比較小,因此應著重討論的將是溫度固定為室溫(298K),在電極固定的情況下,濃度對電極電勢的影響。
離子濃度改變對電極電勢的影響可以通過Cu-Zn原電池的實例來討論。
假若電池反應開始時,Zn2+和Cu2+的濃度為1mol/L,測定電池的電動勢應該是標準狀態的電動勢1.10V。
Zn(s)+Cu2+(1mol/L)=Zn2+(1mol/L)+Cu(s)E=(標準)1.10V
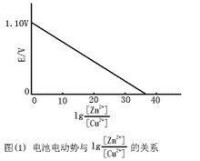
圖1
⑴所示,橫坐標為[Zn2+]和[Cu2+]之比的對數值,縱坐標為電池的電動勢E。Zn2+濃度增大,Cu2+濃度減小時,電池電動勢由1.10直線下降,直到反應達到平衡狀態。
反應達到平衡狀態時,電池停止放電,電池電動勢降低到零;[Zn2+]和[Cu2+]的比值就等於平衡常數K=[Zn2+]/[Cu2+]=10∧37,lg K=37。電池電動勢為零時,直線與橫坐標相交,相交點橫坐標的值約為37。
除上述通過反應的進行可使[Zn2+]/[Cu2+]改變以外,還可有多種改變離子濃度比的方法。如往鋅半電池中加可溶性鋅鹽,用水稀釋或加S2-使Cu2+沉澱濃度降低等等。無論怎樣操作總會發現,只要[Zn2+]/[Cu2+]增加,電池電動勢就會下降;相反,離子濃度比減小,電池電動勢升高。
下面舉例來說明能斯特方程的具體寫法:
⑴已知Fe3++e-=Fe2+,φ(標準)=0.770V
Φ=φ(標準)+(0.0592/1)lg([Fe3+]/[Fe2+])
=0.770+(0.0592/1)lg([Fe3+]/[Fe2+])
⑵已知Br2(l)+2e-=2Br-,φ(標準)=1.065V
Φ=1.065+(0.0592/2)lg(1/[Br-]∧2)
⑶已知MnO2+4H++2e-=Mn2++2H2O,φ(標準)=1.228V
Φ=1.228+(0.0592/2)lg([H+]∧4/[Mn2+])
⑷已知O2+4H++4e-=2H2O,φ(標準)=1.229V
Φ=1.229+(0.0592/4)lg((p(O2)*[H+]∧4)/1)
一、離子濃度改變時電極電勢的變化
根據能斯特方程可以求出離子濃度改變時電極電勢變化的數值
二、離子濃度改變對氧化還原反應方向的影響
非標準狀態下對於兩個電勢比較接近的電對,僅用標準電勢來判斷反應方向是不夠的,應該考慮離子濃度改變對反應方向的影響。
三、介質酸度對氧化還原反應的影響及pH電勢圖