半變異函數

1、半變異函數可定義為:式中:N(h)是以向量h相隔的實驗數據對的數據對數目

文獻來源

2、半方差函數也稱為半變異函數，它是地統計學中研究土壤變異性的關鍵函數，是用來描述土壤性質的空間連續變異的一個連續函數，反映土壤性質的不同距離觀測值之間的變化

文獻來源

3、稱為半變異函數。半變異函數曲線圖(semivariogram)是半變異函數值對距離h的函數圖。它有3個特徵參數：基台值(sill)、變程(range)和塊金值(nugget)[3～5]

文獻來源

4、（h）稱為半變異函數。因模型有m項乘積所以有時亦記為AM－MIm.其中的參數為矩陣D的順序奇異值即

當進行半變異函數建模時，可對自相關性進行檢查和量化。在地統計中，這稱為空間建模，也稱為結構分析或變異分析。在半變異函數的空間建模中，可以從經驗半變異函數圖開始，計算為，

(所有成對位置的相隔距離為 h)。該公式涉及到計算配對位置的差值平方的一半。快速繪製所有配對則變得難以處理。並不繪製每個配對，而是將配對分組為各個步長條柱單元。例如，計算距離大於 40 米但小於 50 米的所有點對的平均半方差。經驗半變異函數是 y 軸上的平均半變異函數值對 x 軸上的距離或步長的圖(請參閱下圖)。

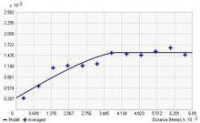
此外，允許複製是內在平穩性假設。因此，可以使用上述半變異函數公式中的平均化。

創建經驗半變異函數之後，可以根據點擬合模型，形成經驗半變異函數。半變異函數建模和在回歸分析中擬合最小二乘直線相似。可以選擇一個函數作為模型，例如，開始上升然後在一定範圍外的較大距離內趨於平穩的球面類型。

目標是計算曲線的參數以根據某些標準最小化與點的偏差。有多種半變異函數模型可供選擇。