奇異積分
奇異積分
奇異積分,又稱考爾德倫-贊格蒙奇異積分運算元,一種特殊的積分變換,他們就最基本與最典型的情形,證明了奇異積分運算元的Lp可積性。奇異積分運算元理論和這一整套的實變函數論方法,不僅在近代調和分析和偏微分方程的理論中,而且在多元複變函數論、概率論和位勢理論中,起著重要的作用。又稱考爾德倫-贊格蒙奇異積分運算元,一種特殊的積分變換,是一維希爾伯特變換到高維歐氏空間的推廣,由A.-P.考爾德倫和A.贊格蒙於1952年引入。Rjƒ稱為ƒ的第j個裡斯變換(j=1,2,…,n)。
目錄
又稱考爾德倫-贊格蒙奇異積分運算元,一種特殊的積分變換,是一維希爾伯特變換到高維歐氏空間的推廣,由A.-P.考爾德倫和A.贊格蒙於1952年引入。他們就最基本與最典型的情形,證明了奇異積分運算元的L可積性。這是奇異積分理論的奠基性工作。以後經E.M.施坦、G.韋斯和C.費弗曼等人,把奇異積分同哈代-李特爾伍德極大函數、面積積分、多元調和函數邊界性質、李特爾伍德-佩利理論聯繫起來,組成了近代調和分析的主要工具。同時由J.J.科恩、L.尼倫伯格和L.赫爾曼德爾等人在奇異積分理論和方法的基礎上,發展出偽微分運算元、傅里葉積分運算元等理論,形成偏微分方程近代理論的一個重要方面。
奇異積分
奇異積分
(1)
奇異積分
奇異積分
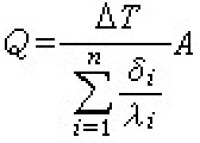
奇異積分
奇異積分
(2)
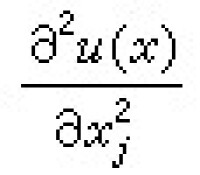
奇異積分
也屬於L。按正常意義是發散的積分(1),用(2)來定義,就可能是收斂的。因此人們稱 (1)右方的積分為奇異積分或奇異積分運算元。
奇異積分
(3)
奇異積分
奇異積分
式中C與ƒ無關。
奇異積分
奇異積分
(4)
奇異積分
表示x與y的內積。
奇異積分
奇異積分
奇異積分
奇異積分
(5)
奇異積分
奇異積分
奇異積分
奇異積分
(6)
奇異積分
奇異積分
奇異積分
結合偏微商和傅里葉變換的關係以及等式(5),就知道里斯變換實際上就是
奇異積分
。
奇異積分
奇異積分
奇異積分
奇異積分
奇異積分
,偏微分運算元僅僅是一種特殊類型的奇異積分運算元。
考爾德倫-贊格蒙分解奇異積分運算元(2)的L有界性的證明,用的是馬欽凱維奇運算元內插定理(見運算元內插)。T的(2,2)型是容易從普朗歇爾等式得到的。困難在於證明T是弱(1,1)型的。為證T的弱(1,1)型,1952年考爾德倫和贊格蒙在他們的奠基性論文中,把函數ƒ∈L分解為g+b)兩部分,其中g有較好的性質,例如g∈L,故稱g為“好的”部分,而b)是“壞的”部分,但具有某些特殊性質,如在某些方塊上的積分為0。這就是通常所說的考爾德倫-贊格蒙分解。在此基礎上,以後發展出一整套的實變函數論方法。奇異積分運算元理論和這一整套的實變函數論方法,不僅在近代調和分析和偏微分方程的理論中,而且在多元複變函數論、概率論和位勢理論中,起著重要的作用。
參考書目
A.P.Calderón and A.Zygmund, On the Existenceof Certain Singular Integrals,Acta MatheMatica,Vol. 88, pp.85~139, 1952.
E.M.Stein,Singular Integrals and Different-iability Properties of Functions,Princeton Univ.Press,Princeton,1970.
E.M.Stein and G. Weiss,Introduction to Fourier Analysis on Euclidean Spaces,Princeton Univ.Press,Princeton,1971.
