單純形法
單純形法
單純形法是求解線性規劃問題最常用、最有效的演演算法之一。單純形法最早由 George Dantzig於1947年提出,近70年來,雖有許多變形體已經開發,但卻保持著同樣的基本觀念。如果線性規劃問題的最優解存在,則一定可以在其可行區域的頂點中找到。基於此,單純形法的基本思路是:先找出可行域的一個頂點,據一定規則判斷其是否最優;若否,則轉換到與之相鄰的另一頂點,並使目標函數值更優;如此下去,直到找到某最優解為止。
單純形法的基本想法是從線性規劃可行集的某一個頂點出發,沿著使目標函數值下降的方向尋求下一個頂點,面頂點個數是有限的,所以,只要這個線性規劃有最優解,那麼通過有限步迭代后,必可求出最優解 。
為了用迭代法 求出線性規劃的最優解,需要解決以下三個問題 :
(1)最優解判別準則,即迭代終止的判別標準 ;
(2)換基運算,即從一個基可行解迭代出另一個基可行解的方法 ;
(3)進基列的選擇,即選擇合適的列以進行換基運算,可以使目標函數值有較大下降 。
原單純形法不是很經濟的演演算法。1953年美國數學家G.B.丹捷格為了改進單純形法每次迭代中積累起來的進位誤差,提出改進單純形法。其基本步驟和單純形法大致相同,主要區別是在逐次迭代中不再以高斯消去法為基礎,而是由舊基陣的逆去直接計算新基陣的逆,再由此確定檢驗數。這樣做可以減少迭代中的累積誤差,提高計算精度,同時也減少了在計算機上的存儲量 。
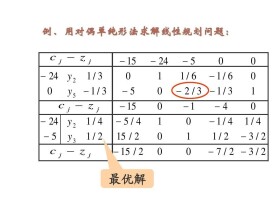
對偶單純形法是使用對偶理論求解線性規劃問題的一種方法,而不是求解對偶問題的一種方法。與對偶單純形法相對應,已有的單純形法稱為原始單純形法 。
原問題與對偶問題解之間的對應關係:即原問題單純形表的檢驗數行對應其對偶問題的一個基本解。單純形法求解的基本思想是:在整個迭代過程中,始終保持原問題的解是可行解,而對偶問題的解可以是非可行解,當對偶問題的解由非可行解變為可行解,也就是原問題的檢驗數行都滿足小於等於零時,原問題取得了最優解。而對偶單純形法的基本思想是:在整個迭代過程中,始終保持對偶問題的解是可行解,原問題的解可以是非可行解,當原問題的解由非可行解變為可行解時,對偶問題取得了最優解。所以,對偶單純形法的實質就是在保證對偶問題可行的條件下向原問題可行的方向迭代 。
數學優化中,由George Dantzig發明的單純形法是線性規劃問題的數值求解的流行技術。有一個演演算法與此無關,但名稱類似,它是Nelder-Mead法或稱下山單純形法,由Nelder和Mead發現(1965年),這是用於優化多維無約束問題的一種數值方法,屬於更一般的搜索演演算法的類別 。
這二者都使用了單純形的概念,它是N維中的N+1個頂點的凸包,是一個多胞體:直線上的一個線段,平面上的一個三角形,三維空間中的一個四面體,等等。
由於目標函數和約束條件內容和形式上的差別,線性規劃問題可以有多種表達式。因此,為了便於討論和制定統一的演演算法,在制定單純形法時,規定使用單純形法求解的線性規劃問題需要有一個標準形式,它有下面三個特徵:
(1) 標準形式目標函數統一為求極大值或極小值,但單純形法主要用來求解極大值;
(2) 所有約束條件(除非負條件外)都是等式,約束條件右端常數項b全為非負值;
(3) 所有變數的取值全為非負值。
下式為滿足上述特徵的線性規劃問題的標準形式:
其中,目標函數中的變數x(x,x,…x)稱為決策變數(控制變數),它的取值受m項資源的限制,它的係數稱為價值係數cs.t.括弧下的內容是約束條件,用b(i=1,···,m)表示第i種資源的擁有量,用aij表示變數xj取值為1個單位時所消耗或含有的第i種資源的數量,通常稱a為技術係數或工藝係數。
除非負條件外的n個約束條件所組成的n元方程組,若可解可求出n個變數xj的值。求出的n個變數所構成的列向量X=(x,···x)若能再滿足非負條件(即決策變數滿足所有約束條件),稱為線性規則問題的可行解。使得目標函數值z達到max最大的可行解即為最優解,求解線性規劃問題的目的就是要找出目標函數的最優解。
下圖為上式標準形式的線性規劃問題的展開型:
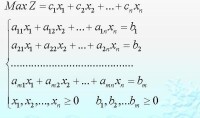
單純形法
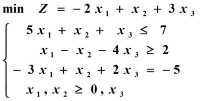
單純形法
(1)目標函數的轉換:統一求極大值,若是求極小值,則可將目標函數乘以(-1),即化為。
(2)變數的轉換:對於已經是大於等於零的變數x≥0不做變化。
對於小於等於零的變數x,取負號令其變為大於等於的變數x',若x≤0,則x'=-x,x'≥0;
若x取值無約束,可令新的兩個非負變數x'和x''相減,即x=x'-x'',其中x',x''≥0。
(3)約束條件的右端項常數的轉換:b<0時,只需將等式或不等式兩端同乘(-1),則
(4)約束條件的轉換:將所有不等式全部轉換為等式。
為此,對於“≤ ”型約束加入一個變數x,對於“≥ ”型約束則減去一個變數x。加到原約束條件中的變數,稱為剩餘變數或鬆弛變數,在實際問題中它表示未被充分利用的資源和超出資源數。由於此部分資源均未轉化為價值和利潤,所以在引進模型后這些變數在目標函數中的係數均為零
此外,為了構造出初始基變數,對於“ = ”型約束和“≥ ”型約束還需要加上人工變數。人工變數構成天然的初始基變數,其係數為1和其它行的人工變數的係數為0(故因此一般省略,不寫出)的特殊構造,組成最簡單的線性無關矩陣——單位矩陣。對於原約束條件中若已有線性無關的基向量,可以不需要再加入人工變數。但為避免出錯和演演算法的統一性,一般情況下面對“ = ”型約束和“≥ ”型約束不應省略人工變數。
按照以上的轉規則,將上述的列線性規劃問題化為標準形式,其結果如下:

單純形法
為了運算簡潔,單純性法的表示與定理的說明往往用矩陣形式說明。上述的標準形式的單純形法用矩形形式表示如下:
其中,C=(c,c,c)為行向量,X=(x,x,x) ,b=(b,···,b)≥0均為列向量;
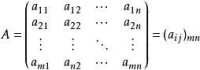
單純形法
且只討論m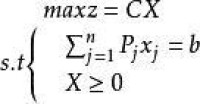 約束方程組的係數矩陣A的任意一個m ×m階的非奇異(滿秩)子方陣B,其列向量線性無關,即方程中任一向量可由這些向量線性表出,故稱為線性規劃的一個基矩陣,簡稱為基。基矩陣B中的每一個列向量P=(j=1,...,m)稱為基向量,與基向量Pj對應的變數x稱為基變數。不失一般性,可假設:
約束方程組的係數矩陣A的任意一個m ×m階的非奇異(滿秩)子方陣B,其列向量線性無關,即方程中任一向量可由這些向量線性表出,故稱為線性規劃的一個基矩陣,簡稱為基。基矩陣B中的每一個列向量P=(j=1,...,m)稱為基向量,與基向量Pj對應的變數x稱為基變數。不失一般性,可假設: 除基變數以外的變數P=(i=m+1,...,n)稱為非基變數。並記非基矩陣為:
除基變數以外的變數P=(i=m+1,...,n)稱為非基變數。並記非基矩陣為: 係數矩陣A可以寫成分塊形式A=(B,N),將基變數的向量記為X=(x,x,···,x) ,
係數矩陣A可以寫成分塊形式A=(B,N),將基變數的向量記為X=(x,x,···,x) ,
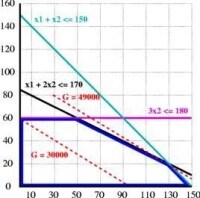 從二維的線性規劃問題的圖解法簡單直觀,有助於了解線性規劃問題的基本原理。非負條件x、x≥0是指坐標軸的第一象限。在以x、x為坐標軸的直角左邊系,,每個約束條件都代表一個半平面。右圖中同時滿足x+x≤150,x+2x≤170,3x≤180和x、x≥0的約束的點,必然落在x1、x2坐標軸和這個三個半平面教程的區域見右圖的藍色框部分,藍色部分區域(包括邊界點的每一個點)都是這個問題的可行解,因此這個區域是線性規劃問題的解集合,稱它為可行域。
從二維的線性規劃問題的圖解法簡單直觀,有助於了解線性規劃問題的基本原理。非負條件x、x≥0是指坐標軸的第一象限。在以x、x為坐標軸的直角左邊系,,每個約束條件都代表一個半平面。右圖中同時滿足x+x≤150,x+2x≤170,3x≤180和x、x≥0的約束的點,必然落在x1、x2坐標軸和這個三個半平面教程的區域見右圖的藍色框部分,藍色部分區域(包括邊界點的每一個點)都是這個問題的可行解,因此這個區域是線性規劃問題的解集合,稱它為可行域。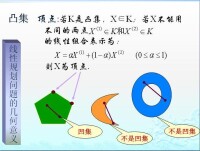
如果向量形式表示係數,那麼即可將矩陣A分塊,A=(P,P,···,P)。可用向量將約束條件改寫為。
故標準形式的單純形法用向量形式表示如下:
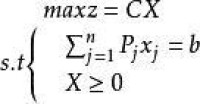
單純形法

單純形法
單純形法
非基變數組成的向量記為,向量X也可以寫成分塊形式
將此A和X的分塊形式帶入到約束方程組AX=b,得。由矩陣的乘法得。又因為B是非奇異矩陣,所以B 存在,將此式兩邊乘以B ,移項后得。可以把X看作一組自由變數(又稱獨立變數),給它們任意一組值,於是。這就是約束方程組的一個解。
特別地,令所有的非基變數為時,則,把約束方程組的這種特殊形式的唯一解,把約束方程組的這種特殊形式的解,稱為基解。或者說,因為滿秩,根據克萊姆法則或高斯消去法,由m個約束變數可解出m個基變數的唯一解。則方程組有唯一解X=(x,...,x) ,將這個解加上非基變數取0的值是Ax=b的一個解:X=(x,x,...,x,0,...,0) ,稱X為線性規劃問題的一個基解或基本解。而滿足標準形式的非負約束條件x≥0的基解稱為基本可行解,簡稱基可行解,對應於基可行解的基稱為可行基。
由此可見,有一個基就可以求出一個基解。基解的非零分量的個數不大於方程個數m,基B的列是從A的n列中選取線性無關的m列,其選法最多共有種,故基的個數或者說一個線性規劃問題的基本解的總數不超過個。

圖解法圖示
對於此例求解得到的最優解,但對一般線性規劃問題,最優解可能出現下列情況:
①有且僅有一個最優解。
②多重最優解,存在著無窮多個最優解,不存在有限最優解;當目標函數平行於非冗餘的緊約束,如果目標函數只有兩個變數,在坐標軸中目標函數一定平行於某一個約束條件。在實踐中,可選擇最優解是有用的,可從眾多解中做出選擇而不會損害最優值。如模型描述的是產品利潤問題,生產兩種產品比生產一種產品在市場競爭中更佔有多樣性的優勢。
③無解或無可行解,其原因在模型的約束條件之間存在著矛盾,模型的構建是不正確的。假如所有的約束都是《類型的並具有非負的右端項,則這種情況永遠不會出現,因為鬆弛變數已經提供了一個可行解。對於其他類型的約束,使用人工變數,只有有一個人工變數在最優迭代中取值為正。
④無界解或無有限最優解,即沒有可行解或各項約束條件不阻止目標函數的值無限增大(或向負的方向無限增大)。這是因為解空間中至少有一個解是無界的,這意味著可以無限制地增加變數的值但不破壞任何一個約束,這種情況下,解空間和最有目標值都是無界的。
⑤退化解,按最小比值θ來確定換出基的變數時,有時出現存在兩個以上相同的最小比值,從而使下一個表的基可行解中出現一個或多個基變數等於零的退化解。退化解出現的原因是模型中存在多餘的約束,使多個基可行解對應同一定點。當存在退化解時,就有可能出現迭代計算的循環,儘管可能性極其微小。
從圖解法可以直觀地看到可行域和最優解的幾何意義:所有可行解構成的集合是凸集,也可能為無界域;它們有有限個頂點,線性規劃問題的每個基可行解對應可行域的一個頂點;若線性規劃問有最優解,必在某頂點上得到。這個結論是通過凸集的定義和三個定理的證明所得出的,下面是詳細的證明過程。
凸集及其頂點
1.凸集

凸集
凸集的概念為,集合K中任意兩個點,其連線上的所有點都是集合K中的點,稱集合K是凸集。雖然對簡單的集合形體可以直觀地判斷其凹凸性,但在高維空間,只能給出點集的解析表達式,因此只能用數學解析式判斷。設K是n維歐式空間的一點集,若任意兩點X∈K,X∈K,其連線可表示為 則稱K為凸集。
2.凸組合
設X,X,···,X是歐式空間E 中的k個點。若存在μ,μ,μ且0≤μ≤1,i=1,2,···,k; ,使X=μX+μX+···+μX則稱X為X,X,···,X的凸組合。
3.頂點
凸集K中滿足下述條件的點X稱為頂點:如果K中不存在任何兩個不同的點X,X,使X成為這兩個點連線上的一個點。或者這樣敘述:對於任何X∈K,X∈K,不存在,則稱X是凸集K的頂點。
定理一
若線性規劃問題存在可行解,則問題的可行域 是凸集。
證:為了證明滿足線性規劃約束條件 的所有點組成的幾何圖形D是凸集。只要證明D內任意兩點X,X的連線上的點也必定在D內即可,下面給予證明。
設X=(x,x,...,x) ,X=(x,x,...,x) 為D內任意兩點,即X∈D,X∈D,且X≠X。
將X,X帶入約束條件AX=b,則有
由凸集的定義,X,X連線上任意一點可以表示為:X=aX+(1-a)X(0
兩邊同乘A:AX=A[aX+(1-a)X],將此式用向量展開式表示:
所以集合中任何兩點連線上的點滿足約束條件,即均在集合內,即X=aX+(1-a)X∈D,所以可行域是凸集。
引理一
線性規劃問題的可行解X=(x,x,...,x) 為基可行解的充要條件的是X的正分量所對應的係數列向量是線性獨立的。
證(1)必要性:由於基解的列向量是線性獨立的,並且可行解的分量即是正分量。
(2)充分性:若向量P,P,···,P線性獨立,則必定k≤m;當k=m時,它們恰構成一個基,從而X=(x,x,...,x,0...0)為相應的基可行解。當k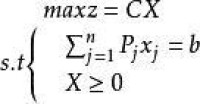 在約束條件的變數的係數矩陣總會存在一個單位矩陣作為初始可行基
在約束條件的變數的係數矩陣總會存在一個單位矩陣作為初始可行基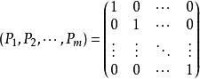 這是因為當線性規劃的約束條件均為≤號,利用化為標準型的方法,在每個約束條件的左端加上一個鬆弛變數。經過整理,重新對x和a(i=1,2,···,m;j=1,2,···,n)進行編號,可得到以下方程組。
這是因為當線性規劃的約束條件均為≤號,利用化為標準型的方法,在每個約束條件的左端加上一個鬆弛變數。經過整理,重新對x和a(i=1,2,···,m;j=1,2,···,n)進行編號,可得到以下方程組。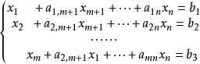
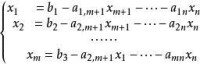
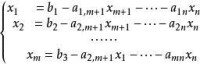 對線性規劃問題的求解結果可能出現唯一最優解、無窮多最優解、無界解和無可行解四種情況,為此需要建立對解的判別標準。一般情況下,經過迭代之後變成
對線性規劃問題的求解結果可能出現唯一最優解、無窮多最優解、無界解和無可行解四種情況,為此需要建立對解的判別標準。一般情況下,經過迭代之後變成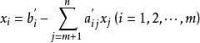 一般式為
一般式為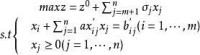 其中,稱σ為檢驗數或判別數,它是典式的目標函數的非基變數x(j=m+1,···,n)的係數,它又表示當某個非基變數的值改變1個單位,所引起的目標函數值的該變數,因此又稱為相對價值係數。
其中,稱σ為檢驗數或判別數,它是典式的目標函數的非基變數x(j=m+1,···,n)的係數,它又表示當某個非基變數的值改變1個單位,所引起的目標函數值的該變數,因此又稱為相對價值係數。
 用單純形法求解線性規劃問題所需的迭代次數主要取決於約束條件的個數。如今一般的線性規劃問題都是應用單純形法標準軟體在計算機上求解,對於具有106個決策變數和104個約束條件的線性規劃問題已能在計算機上解得。
用單純形法求解線性規劃問題所需的迭代次數主要取決於約束條件的個數。如今一般的線性規劃問題都是應用單純形法標準軟體在計算機上求解,對於具有106個決策變數和104個約束條件的線性規劃問題已能在計算機上解得。
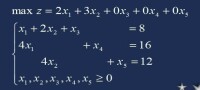 由於都為"≤"型,所以在三個約束式分別加上三個剩餘變數x、x、x,將不等式轉化為等式。
由於都為"≤"型,所以在三個約束式分別加上三個剩餘變數x、x、x,將不等式轉化為等式。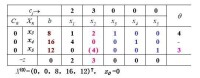 第三步:更換基變數
第三步:更換基變數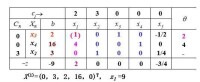 第四步:繼續迭代。
第四步:繼續迭代。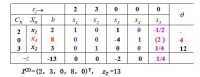 第五步:確定所有檢驗數σ≤0,計算最優值Z*。
第五步:確定所有檢驗數σ≤0,計算最優值Z*。
定理二
(極點與基可行解的等價性定理)線性規劃問題基可行解X對應於線性規劃問題可行域(凸集)D的頂點。
證:本定理需要證明:X是可行域頂點⇔X是基可行解,這一定理可由反證法證明。即證明:X不是可行域的頂點⇔X不是基可行解。
不失一般性,假設基可行解X的前m個分量為正。故。
分兩步來討論,分別用反證法。
(1)若X不是基可行解,則它一定不是可行域D的頂點。
根據引理1,若X不是基可行解,則其正分量所對應的係數列向量P,P,···,P線性相關,即存在一組不全為零的數α,i=1,2,···,m 使得αP+αP+···+αP=0。
用一個μ>0的數乘以上式,再分別與 相加或相減,分別得到下列兩式:
(x-μα)P+(x-μα)P+···+(x-μα)P=b
(x+μα)P+(x-μα)P+···+(x-μα)P=b
現取X=[(x-μα),(x-μα),···,(x-μα),0,···0]
X=[(x+μα),(x-+μα),···,(x-+μα),0,···0]
可以得出X=X/2+X/2,即X是X1,X2連線的中點。
另一方面,當μ充分小時,可保證x+μα≥0,i=1,2,···,m
即X,X是可行解。這證明了X不是可行域D的頂點。
(2)若X表示可行域D的頂點,則它一定不是基可行解。
因為X=(x,x,...,x,0...0)不是可行域D的頂點,故在可行域D中找到不同的兩點Y和Z,使,或可寫成。
因為Y和Z是可行域的兩點,應滿足:
將這兩式相減,即得
因Y≠Z,所以上式係數y-z不全為零,故向量組P1,P2,···,Pm線性相關,與假設矛盾。即X不是基可行解。
推論:設 的秩為m,在非退化情況下,則X是S的頂點的充要條件是X的非0元為m個。
定理三
設線性規劃問題有解,一定存在一個基可行解是最優解,由定理二可知必在可行域D={X|AX=b,X≥0}的某個頂點上取得最優值。這個定理分為三個部分。
定理3.1若一個問題(LP)有可行解,則它必有基可行解。
證 設X是線性規劃問題的一個可行解,如果其正分量所對應的列向量P,P,···,P線性無關,由引理一可知,X是一個基可行解,定理成立。否則,需證明:從X出發,必可找到LP的一個基可行解。
因為P1,P2,···,Pk線性相關,即存在不全為零的數δ,δ,···,δ,使得。
則X在可行域內必能找到兩點,X=X+εб,X=X-εб ,其中δ=(δ,δ,···,δ,0,···,0)
其中有δ≠0,取,且必有x±εб≥0(j=1,2,···,n) ,即X≥0,X≥0。
又因為,所以,
故有AX=b,AX=b,所以X,X是LP的兩個可行解。
再由ε的取法可知,x±εб≥0中,至少有一個等於零,於是所做的可行解X和X中,它的非零分量至少比X的減少1。如果這些非零分量所對應的列向量線性無關,則X和X為基可行解,定理成立。
否則,又可以X或X出發,重複上述步驟,再構造一個新的可行解X或X,使它的非零分量的個數繼續減少。這樣經過有限次重複之後,比可找到一個可行解X或X,使它的非零分量對應的列向量線性無關。因為在最壞的情況下,只有一個非零分量時,對應的只有一個非零的列向量,它必然是線性無關的,故X或X必為基可行解。
定理3.2若線性規劃問題有最優解,一定存在一個基可行解是最優解。
證 設X是線性規劃的一個最優解,Z=CX是目標函數的最大值。若X不是基可行解,由定理二可知,X不是頂點,一定能在通過X的直線上的另外兩個點,將這兩個點帶入目標函數有
C(X+εδ)=CX+Cεδ , C(X-εδ)=CX-Cεδ
因CX為目標函數的最大值,故有CX≥CX+Cεδ ,CX≥CX-Cεδ
Cεδ不可能為正數或負數,因此Cεδ=0,即有C(X+εδ)=CX=C(X-εδ)。
如果(X+εδ)或(X-εδ)仍不是最優解,按上面方法繼續做下去,則根據定理3.1的證明方法,它的非零分量的個數比X的減少1。在最壞的情況下,只有一個非零分量時,對應的只有一個非零的列向量,它必然是線性無關的。所以一定可以找到一個基可行解,其目標函數值等於CX,問題得證。
根據定理二和定理三,可以得出如下結論:
推論一:若問題的可行域有界,則此問題的最優解一定可以在其可行域D的頂點上達到。
定理3.3設問題(LP)在多個頂點X,X,···,X出達到最優,則任意一點 也是(LP)的最優解。
證 設目標函數的最優值為Z,則有假設有CX=Z
由上式可知,有
故任意一點X也是LP的最優解。X稱為X,X,···,X的凸組合。
這定理說明若問題有兩個或多於兩個的最優解,則它就有無窮多個最優解。另外,若問題的可行域無界,則可能無有限解,也可能有有限解。若有有限解,則必可在可行域的某個頂點上達到。
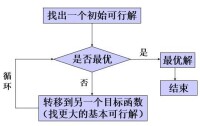
由上述的定理3可知,如果線性問題存在最優解,一定有一個基可行解是有最優解。因此單純形法迭代的基本思路是:先找出一個基可行解,判斷其是否為最優解。如為否,則轉換到相鄰的基可行解,並使目標函數值不斷增大,一直找到最優解為止。
初始可行基確定
對於標準型線性規劃問題
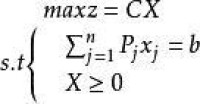
單純形法
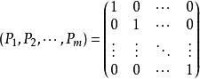
單純形法
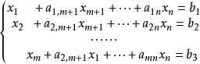
單純形法
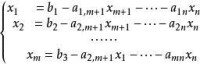
單純形法
移項可得
其鬆弛變數x.···,x的係數矩陣顯然為m×m單位矩陣。令x=x···=x=0,可得x=b(i=1,2,···m),又因為b≥0,所以得到一個初始基可行解。
對約束條件為≥或=的情況,為便於初始基可行解,可以構造人工基,人為產生一個單位矩陣,可參見人工變數法。
最優性檢驗
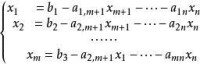
單純形法
單純形法
將其帶入目標函數,整理后得
令,於是
再令σ=c-z(j=m+1,···,n),則
因此可以將線性規劃問題的標準形式化為典式:
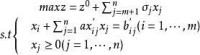
單純形法
1.最優解的判別定理
設X =(b',b',···b',0,···,0) 為對應基B的一個基可行解,且對於一切j=m+1,···,n,有σ≤0,或用向量表示σ=(0,···,0,σ,σ,···,σ)≤0,則X為最優解。
證:設X為線性規劃的任一可行解,X≥0,σ≤0,σX≤0,從而最大值z*=CX =z ≥z +σX=CX=z。
因為x為正數,當σ≤0,當迭代恰好會使得z會變小(無法更優),其解即為最優。
因此σ≤0稱為最優性條件,它是判別當前接是否為最優解的標準。檢驗數還可以寫成矩陣形式σ=(σ,σ)=C-CB A=(0,C-CB N)≤0,其中σ=0為基變數對應的檢驗數向量;σ=C-CB N為非基變數對應的檢驗數向量。這說明基變數的檢驗數必為0,並且非基變數的檢驗數都為負數時,才有唯一最優解。
2.無窮多最優解判別定理
若X =(b',b',···b',0,···,0) 為一個基可行解,對於一切j=m+1,···,n,又存在某個非基變數的檢驗數σ=0,則線性規劃問題有無窮多最優解。
證 只需將非基變數x換入基變數中找到一個新基可行解X 。σ=0,z=z,故X也是最優解。故X也是最優解。根據定理3.3可知X 和X 連線上所有點都是最優解,故有無窮多最優解。
3.基可行解的改進定理
若初始可行解X不是最優解時,需要找一個新的可行基。具體做法是從原可行解基換一個列向量(當然要保證線性獨立),得到一個新的可行基,這稱為基變換。為了換基,先要確定換入變數,再確定換出變數,讓它們相應的係數向量進行對換,就得到一個新的基可行解。
定理內容:X =(b',b',···b',0,···,0) 對應於基B的一個基可行解,若滿足下列條件:
(1)有某個非基變數x的檢驗數σ>0(m+1≤k≤n);
(2)a(i=1,2,···,m)不全小於或等於零,即至少有一個a>0(1≤i≤m);
徠(3)b'>0(i=1,2,···,m),即X 為非退化的基可行解。則從X 出發,一定能找到一個新的基可行解X ,使得CX >CX 。
證 我們採用一種構造性的證明方法,即將X具體地找出來,為此,我們作換基運算:
由,當某些σ>0時,增加則目標函數還可以增大,這時要將某個非基變數xj喚到基變數中去,稱為換入變數。
3.無界解判別定理
若X=(b',b',···b',0,···,0) 為一基可行解,有一個σ>0,並且對i=1,2,···,m,都有a‘≤0,那麼該線性規劃問題具有無界解(或稱無最優解)。
證 構造一個新的解X,它的分量為x=b‘-λα‘(λ>0)
x=λ
x=0,j=m+1,···,n
因a‘≤0,所以對任意的λ>0都是可行解,把x帶入目標函數內得z=z+λσ。
因σ>0,λ→+∞,則z→+∞,故該問題目標函數無界。
為檢驗一個基可行解是否最優,需要將其目標函數值與相鄰基可行解的目標函數進行比較。為了書寫規範和便於計算,對單純形法的計算設計了一個種專門表格,稱為單純性表。迭代計算找出一個新的基可行解,就畫一張單純形表。含初始基可行解的單純形表,稱為初始單純形表,含最優解的單純形表,稱為最終單純形表。下圖即為單純形表的一般格式。
| Cj→ | X | ... | c1 | ... | cm | ... | cj | ... | cn |
| C | 基 | b | x | ... | x | ... | x | ... | x |
| c | x | b | 1 | ... | ... | a | ... | a | |
| c | x | b | ... | ... | a | ... | a | ||
| ... | ... | ... | ... | ... | ... | ... | |||
| c | x | b | ... | 1 | ... | a | ... | a | |
| c-z | ... | ... | ... | ||||||
單純形表結構為:表的第2行列出所有基變數,表的第1-3列分別列出基可行解中基變數係數、基變數和每個約束的取值(右端值)。表的第4-6列寫在基變數下面是單位矩陣,非基變數x下面數字是該變數係數向量P表示為基向量線性組合時的係數,即化出單位矩陣后的係數。因為P,...,P是單位向量,故有:
最後一行(c-z)寫的是檢驗數σ例如求第j列的檢驗數,只需將變數x的係數即數字(a,...,a)與C中同行的數字(c,...,c)分別相乘加和,再用它上端的c值減去乘積加和,即可得出:
單純形法的一般解題步驟可歸納如下:
①把線性規劃問題的約束方程組表達成典範型方程組,典範型方程組要實現變數轉換(所有變數為非負)、目標轉換(統一為求極大值,若求極小值可乘以(-1))、約束轉換(由不等式轉化為等式)。然後,找出基本可行解作為初始基可行解。列出初始單純形表。
②若基本可行解不存在,即約束條件有矛盾,則問題無解。
③若基本可行解存在,從初始基可行解作為起點,根據最優性條件和可行性條件,引入非基變數取代某一基變數,找出目標函數值更優的另一基本可行解。
④按步驟3進行迭代,直到對應檢驗數滿足最優性條件(這時目標函數值不能再改善),即得到問題的最優解。
⑤若迭代過程中發現問題的目標函數值無界,則終止迭代。
圖示表示如下:

單純形法的一般求解步驟
例1:求解下述線性規劃問題,只有唯一最有解的情況。
第一步:將一般形式轉換為標準形式:
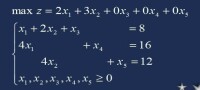
例題1
第二步:列出初始單純形表。
下圖為一張完整的單純形表,不同的教材畫法有所差異,例如可以省略對b值和θ的部分單獨進行列式計算。這裡用最為全面的畫法進行講解。其中紅色部分為約束條件原本的常數值,最後一行為檢驗數。中間的數值為各個變數的原始數值,其中基變數的係數,即藍色數值(3×3)恰好構成一個單位矩陣,其檢驗數也恰好都為0。

例一步驟1
最後一行中x、x檢驗數為不為負數或零,因此尚未取得最優值。需要去找另一個基本可行解,即將非基變數換入基變數中。如此循環下去,直到找到最優解為止。
通過基變數換入換出的操作需要有兩個原則。第一,如果有多個檢驗數為正,那麼從最大的一個開始調整,因為變動檢驗數大的變數對於z值的變化越大,這道題目中x的這一列的檢驗數最大,因此選擇x入基變數。但是為了保證係數的非負,b值與係數的比值θ即最右邊的一行,應該選擇數值最小的一個,因此這裡選擇4(<5),因此x為出基變數。由3(最大檢驗數σ)和3(最小比值θ)確定的數值4稱為主元,進行變換的方法稱為高斯消元法,即用行的初等變換進行列消元。

例一步驟2
消元后x、x、x變成基變數,同時係數和b值也發生了相應的變化,計算出檢驗數。發現x的檢驗數仍為正數,將x作為入基變數。通過θ最小法則,確定x5為出基變數。繼續畫出消元后的單純形表。

例一步驟3

例一步驟4
在採用Bland's法則選擇用於轉軸操作的d和e(相同值的情況下取字典序最小)之後,可以證明單純形法一定能夠在有限步之後終止,但是最壞情況演演算法的時間複雜度為指數級別的,而且可以構造出讓單純形法的時間複雜度達到指數級別的具體實例。不過實踐證明在絕大多數情況下單純形法的效率非常令人滿意。
單純形法的最壞時間複雜度為指數級別,並不意味著線性規劃不存在多項式級別的演演算法。橢球演演算法和內點演演算法均為解決線性規劃的多項式時間演演算法。
如今線性規劃的理論與演演算法均非常成熟,在實際問題和生產生活中的應用非常廣泛;線性規劃問題的誕生標誌著一個新的應用數學分支———數學規劃時代的到來。過去的 60 年中,數學規劃已經成為一門成熟的學科。其理論與方法被應用到經濟、金融、軍事等各個領域。數學規劃領域內,其他重要分支的很多問題是在線性規劃理論與演演算法的基礎上建立起來的,同時也是利用線性規劃的理論來解決和處理的。由此可見,線性規劃問題在整個數學規劃和應用數學領域中佔有重要地位。因此,研究單純形法的產生與發展對於認識整個數學規劃的發展有重大意義。
目錄