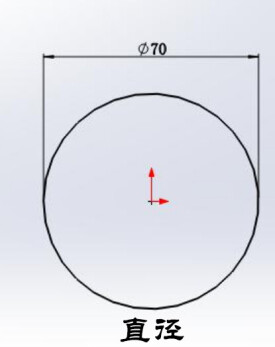
直徑
平面圖形中心到邊上兩點的距離
直徑是通過圓心且兩個端點都在圓上任意一點的線段。一般用字母d(diameter)表示。
直徑所在的直線是圓的對稱軸。
直徑的兩個端點在圓上,圓心是直徑的中點。直徑將圓分為面積相等的兩部分,中間的線段就叫直徑(每一個部分成為一個半圓)。
在同一個圓中直徑的長度是半徑的2倍,可以表示或
證明:設有直徑AB,根據直徑的定義,圓心O在AB上。
並且,在同一個圓中弦長為半徑2倍的弦都是直徑。即若線段d=2r(r是半徑長度),那麼d是直徑。
反證法:假設AB不是直徑,那麼過點O作直徑AB',根據上面的結論有
(等邊對等角)
又∵AB'是直徑,(直徑所對的圓周角是直角)
那麼△ABB‘中就有兩個直角,與內角和定理矛盾
∴假設不成立,AB是直徑
在同一個圓中直徑是最長的弦。
證明:設AB是的直徑,CD是非直徑的任意一條弦,則可證明AB>CD恆成立。
連接OC、OD,根據圓的定義,
∵CD不是直徑
∴CD不經過圓心O,即O、C、D三點可以構成三角形
在中,根據三角形三邊關係可知
即AB>CD
直徑
直徑
圓的面積公式:半徑的平方乘π(即:)