入射角

公元1世紹，正在亞歷山大城學習的古希臘數學家海倫發現：光在鏡面上反射時，入射角等於反射角。這是為什麼呢？海倫認為，這是因為光總是沿著最快的路徑傳播，而自然界所發生的事情都遵循最快、最好的原則。海倫長期研究光的傳播，並打算整理自己研究的成果，發行一本關於鏡子與光學的書。

海倫既是一位數學家，也是一位物理學家，生活在公元1世紀的埃及亞歷山大城。他留下了很多數學和科學方面的偉大成果。早在1900多年前，海倫就已經發明出了能自動打開的門，能自己表演的木偶，以及能連續射箭的武器。

他在天文學方面最著名的成就是，根據在各個地區測定的月球的位置，確定了亞歷山大城與羅馬的距離。

入射角性質

正如前面所介紹的，海倫通過研究光線的傳播，發現了光在鏡面上反射時，入射角與反射角相等。入射角是指射到鏡面上的光線與法線所形成的夾角，反射角是指被鏡面反射的光線與法線形成的夾角，法線是過入射點垂直於鏡面的直線。光線被鏡面反射的傳播路線可以用下圖表示，其中，ADP為入射角，

PDB為反射角。

從A處發出的光線在點D處被鏡面反射至B。如果光線在點D處沒有被反射，而是沿直線傳播，則射向C。此時，B到E的距離等於E到C的距離，點B和點C關於鏡面成軸對稱。因此，全等。由此可知，與大小相等。

如果光線在D處沒有被反射，而是徑直射向C處，和是對頂角，因為對頂角大小相等，所以和大小相等。

因為和分別與相等，所以得出結論：與大小相等。

∠1的餘角就是入射角，∠2的餘角就是反射角。因為，因此入射角和反射角也相等。

入射角=反射角

海倫知道光沿直線傳播，因此能發現入射角等於反射角的原理。

下圖是反射原理的例子：

反射原理——反射角等於入射角

材料：白紙，鏡子，直尺，量角器

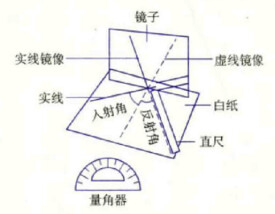
用直尺在白紙上畫一條虛線，再畫一條與虛線相交的實線，在兩線交點的位置上豎直放一面鏡子。轉動鏡子，使虛線和它的鏡像在一條直線上，則紙上原先畫好的實線與虛線的夾角為人射角。如圖1所示。

現在，往鏡子里看，找到實線鏡像。在白紙上把與虛線相交的實線鏡像線延長，這條實線的鏡像延長線與紙上虛線的夾角叫反射角。

測量紙上入射角和反射角的大小，你會發現：二者大小相等，即入射角等於反射角。

在紙上畫出不同大小的相交實線與虛線的角度，重複以上實驗，以證實入射角等於反射角是普適的。