可積函數
數學中的概念
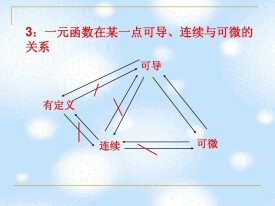
如果f(x)在[a,b]上的定積分存在,我們就說f(x)在[a,b]上可積。即f(x)是[a,b]上的可積函數。
定理1 設f(x)在區間[a,b]上連續,則f(x)在[a,b]上可積。
定理2 設f(x)在區間[a,b]上有界,且只有有限個間斷點,則f(x)在[a,b]上可積。
定理3 設f(x)在區間[a,b]上單調有界,則f(x)在[a,b]上可積。
有限。令
為f的"正部"和"負部"。如果f可積,則其積分定義為
對於實數 p≥ 0,函數f是p-可積的如果|f| 是可積的;對於p= 1,也稱絕對可積。(注意f(x)是可積的
當且僅當|f(x)|是可積的,所以"可積"和"絕對可積"在勒貝格意義下等價。)術語p-可和也是一樣的意義,常用於f是一個序列,而μ是離散測度的情況下。
這些函數組成的L空間是泛函分析研究中的主要對象之一。