數學模式論
數學模式論
《數學模式論》是有關對數學的學習過程進行研究的理論的一篇論文。
數學模式論(mathematical model theory)運用邏輯形式方法,即建立一定的有關學習數學的邏輯模式,對數學的學習過程進行研究的理論。
關於學習過程的數量分析的理論,在美國心理學家C.L.赫爾的著作中已有某些綱領性的敘述。但是,數學模式論則是20世紀50年代初期由美國W.K.埃斯蒂斯等人所創立的。1951年,埃斯蒂斯發表了關於刺激樣本理論的第一篇文章,以後又繼續進行了大量的研究。一般認為,埃斯蒂斯是數學模式論的代表人物。
數學模式只是用來探討學習的理論結構的一種特殊方法,並非一種新的關於學習的基本原理。具有不同觀點的心理學家均可運用數學的方法來完善他們的理論。
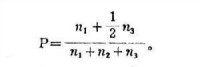
圖一
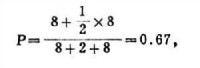
圖二
在學習的研究中運用數學方法,可以發現實驗數據之間的邏輯聯繫。數學模式既可用來簡潔地表示關於學習過程的資料,又可用來解釋這些資料。因此,在一定的條件下,運用數學模式可以精確地預測學習的進程。例如,我們可以預測對複合刺激物的反應。如果我們以S1表示複合刺激物中的一組要素與反應 A1相聯繫; S2與 A2相聯繫; S3表示第三組要素,其中,任意的1/2要素與 A1聯繫,1/2要素與 A2聯繫。這樣,如果考查由S1中的 n1要素, S2中的 n2要素, S3中的 n3要素組成的複合刺激,那麼,預期 A1反應的比例是 圖一。斯科弗勒爾(Schoeffler)在1954年用實驗檢驗了這一預測。他在一次測驗中分別從S1、 S2、 S3中提取 8、2、8個要素,這個預測值是圖二 與觀察所得值0.67相同。因此,有些主張在學習的研究中運用數學方法的人認為,某些學習的數學模式的精確性甚至可以與最佳的物理理論相比。其理由是邏輯性合理高於任何的理論性合理
但是,當前所採用的一些數學模式也有一定的缺陷。現在還沒有一個在任何情況下都能適用的模式。往往是在A情況下所得到的數學模式並不適合或不完全適合情況B;而且,現在所有到的應用模式僅是單獨的,不連貫的的模,尚缺乏一個全面的聯結系統用以涵蓋眾多類型的統領模式。
但是,在心理學中運用數學模式已經滲透到許多研究領域之中,所以,在學習的過程中運用數學模式這一潮流還將繼續下去。
“數學模式論”是我國影響最大的數學哲學理論,這一理論對數學的真理性問題做了深入的探討,給出了三種解釋。
人們往往會對這樣的事實情不自禁地感到驚奇:當初由人腦概念思維(即抽象分析思維活動)所產生的數學模式,甚至抽象度極高的模式,為什麼最終居然能和現實世界中的事物關係結構規律相一致呢?對此問題一個最具概括性的回答是:那是由於人腦抽象思維形式和客觀世界中的關係結構形態具有同構關係的緣故,但是,為什麼主觀世界、客觀世界之間能夠存在這種美妙的同構關係呢?對此就只能用反映論的基本原理來作出解釋了:上述同構關係之所以存在,歸根結底可以說是由宇宙世界中的物質運動規律的統一性所決定的,事實上,具有概念思維形式並可能動地反映事物關係結構規律的人腦反映機制,其本身就是遵循物質運動的普遍規律進化而成的最高物質組成形式周此,由它所表現出來的思維運動規律必然對應地符合宇宙世界中的具有統一性的普遍運動規律。
然而,用“同構”來說明如此複雜的現象未免過於簡單,並且,重要的是我們要知道,二者為什麼會同構?而對於這一點,上述解釋難以令人滿意:每個人的大腦都是“遵循物質運動的普遍規律進化而成的最高物質組成形式”,照這種解釋,豈不是每個人的“概念思維所產生的數學模式”都必定與“現實世界中的事物關係結構規律”相一致?
在現代社會中,每個數學家都必然地是作為相應的社會共同體(可特稱為“數學共同體”)的一員從事研究活動的,從而就自覺地或不自覺地處在一定的數學傳統之中,特殊地,一種數學模式的最終建立也就取決於數學共同體的“判決”:只有為數學共同體一致接受的數學概念、方法、問題等才能成為真正的模式(從而,所說的建構活動事實上也就是一種“社會的建構”)。
這就是說,“數學共同體”的“判決”保證了數學模式的正確性,那麼,如果“數學共同體”反對的模式也能成為真正的模式,這種判決就沒有意義了,然而事實是,歷史上曾多次出現真正的數學模式遭到“數學共同體”強烈反對的事例:發現無理數的人被他的同事扔進大海;非歐幾何在創立后的三十多年裡一直被當做異端邪說;虛數長期得不到數學界的承認,甚至到了19世紀,還有數學家對虛數的使用感到極大的不安;就連負數最初也遭到包括韋達在內的許多數學家的反對,類似的例子還可舉出很多,當然,“數學共同體”最後都承認了這些模式,但那是因為後來的事實證明了這些模式確實是真理,以至於“數學共同體”不得不承認它們,這就說明,檢驗數學模式的真理性另有標準,並不取決於“數學共同體”的“判決”。
就其最基礎的部分而言,數學是建立在直接經驗之上的,而這種聯繫也就直接保證了這部分數學在經驗活動中的可應用性,……就數學的高級部分而言,儘管這在一定意義上可以看成思維的自由想象與創造,而並非建立在客觀實在的直接抽象之上,但是,這種思維活動又是以已建立的數學概念或理論為基礎的,從而,這些高度抽象的概念和理論也就通過初等數學的過渡與現實世界有著較為直接或間接的聯繫,”
這就是說,數學與客觀現實的直接或間接的聯繫保證了它的正確性,數學的高級部分確實是由數學的低級部分發展而來的,數學的低級部分確實與客觀現實有著直接的聯繫,但是,僅靠與客觀世界的聯繫就能確保數學的真理性嗎?各種自然科學都與客觀世界有著密切的聯繫,但是,這些科學都是在不斷地修正自己的理論中前進的,這種聯繫顯然並不能保證它們的真理性,那麼,是不是數學有什麼得天獨厚的地方呢?