反對稱矩陣
反對稱矩陣
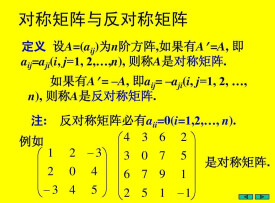
反對稱矩陣定義是:A=-A’(A的轉置前加負號),它的第Ⅰ行和第Ⅰ列各數絕對值相等,符號相反。且主對角線上的元素為均為零。
設A為n維方陣,若有A'=-A,則稱矩陣A為反對稱矩陣。對於反對稱矩陣,它的主對角線上的元素全為零,而位於主對角線兩側對稱的元反號。反對稱矩陣具有很多良好的性質,如若A為反對稱矩陣,則A',λA均為反對稱矩陣;若A,B均為反對稱矩陣,則A±B也為反對稱矩陣;設A為反對稱矩陣,B為對稱矩陣,則AB-BA為對稱矩陣;奇數階反對稱矩陣的行列式必為0。反對稱矩陣的特徵值是0或純虛數,並且對應於純虛數的特徵向量的實部和虛部形成的實向量等長且互相正交。
對稱矩陣定義是:A=A‘(A的轉置)
對稱矩陣的元素A(i,j)=A(j,i).特性斜對稱矩陣自身相乘的積是對稱矩陣。任意矩陣A,AT?A是斜對稱矩陣。若A是斜對稱矩陣,x是向量,xTAx=0斜對稱矩陣的主對角線元素必是零,所以其跡數為零。行列式若A是的斜對稱矩陣,其行列式滿足若n是奇數,行列式等於零。這個結果叫雅可比定理。若n是偶數,行列式可以寫成部分元素的多項式的平方:。這個多項式叫A的Pfaffian。任意實斜對稱矩陣的行列式是非負數。譜理論斜對稱矩陣的特徵根永遠以成對的形式(±λ)出現,因此一個實數斜對稱矩陣的非零特徵根為純虛數將會如下:iλ1,?iλ1,iλ2,?iλ2,…,其中λk是實數。實斜對稱矩陣是正規矩陣(它們與伴隨矩陣可交換),因此滿足譜定理的條件,它說明任何實斜對稱矩陣都可以用一個酉矩陣對角化。由於實斜對稱矩陣的特徵值是複數,因此無法 用實矩陣來對角化。然而,通過正交變換,可以把每一個斜對稱矩陣化為方塊對角線的形式。特別地,每一個2n×2n的實斜對稱矩陣都可以寫成A=QΣQT的形式,其中Q是正交矩陣,且:對於實數λk。這個矩陣的非零特徵值是±iλk。在奇數維的情況中,Σ總是至少有一個行和一個列全是零。
設,若其中元素滿足,則稱A是對稱矩陣;若其元素滿足,則稱A為反對稱矩陣。
若A是反對稱矩陣,則,當時,便有,即反對稱矩陣主對角線上的元全為零,而位於主對角線兩側對稱的元反號。
反對稱矩陣性質1
設A,B為反對稱矩陣,則A±B仍為反對稱矩陣。
證明過程:
設A,B為反對稱矩陣,即有
則
至此,根據反對稱矩陣的定義可得,A±B為反對稱矩陣。
反對稱矩陣性質2
設A為反對稱矩陣,則仍為反對稱矩陣。
證明過程:
設A為反對稱矩陣,即有
則有
至此,根據反對稱矩陣的定義可得,仍為反對稱矩陣。
反對稱矩陣性質3
設A為反對稱矩陣,B為對稱矩陣,則AB-BA為對稱矩陣。
證明過程:
已知A為反對稱矩陣,B為對稱矩陣,即有
故有:
至此,根據反對稱矩陣的定義可得,AB-BA為對稱矩陣。
反對稱矩陣注意事項
(1)設A,B為反對稱矩陣,AB不一定是反對稱矩陣。
(2)設A為反對稱矩陣,若A的階數為奇數,則A的行列式為0;A的階數為偶數,則根據具體情況計算。
反對稱矩陣定理1
奇數階反對稱矩陣的行列式必為0。
證明過程:
設A為反對稱矩陣,即有
設A為反對稱矩陣,即有
故有
當n為奇數時,就由,於是。
反對稱矩陣定理2
反對稱矩陣的特徵值是0或純虛數,並且對應於純虛數的特徵向量的實部和虛部形成的實向量等長且互相正交。
證明:
(1)設實反對稱矩陣A的特徵值,相應的特徵值向量,其中u,v是實向量。那麼由得到
即
分別等置兩邊的實部和虛部得到
於是
因為(內積),所以上二式相加得到
又因為,所以
從而。類似地可以知道。因此
於是由推出a=0,從而。
(2)由(1)中可得,所以,即
於是
因為,所以。
此外。由以及可知,即u,v正交。