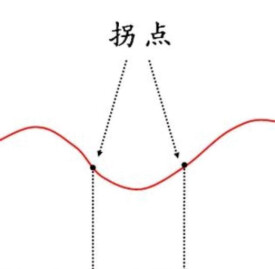
拐點

設函數在點的某鄰域內連續，若（，）是曲線凹與凸的分界點，則稱（，）為曲線的拐點。

註：拐點（，）是曲線上的一點，它有橫坐標和縱坐標，不要只把橫坐標當成拐點。

設函數f（x）在點的某鄰域內具有二階連續導數，若（，）是曲線的拐點，則,但反之不成立。

直接根據拐點的定義，可以得到曲線存在拐點的第一充分條件。

設函數f（x）在點的某鄰域內具有二階連續導數，若的兩側異號，則（，）是曲線的一個拐點；若的兩側同號，則（，）不是曲線的拐點。

設函數在點處，但，那麼存在的一個領域，在該領域內或，根據函數單調性判定定理，則在該鄰域內單調遞增或單調遞減，而，故存在點的一個鄰域，在點的兩側異號，從而判定為曲線的拐點的橫坐標。根據以上分析，可以得到曲線存在拐點的第二充分條件。

若，且,則（，）是曲線的拐點。

除上述情況外，f（x）的二階導數不存在的點也有可能是的符號發生變化的分界點。

可以按下列步驟來判斷區間I上的連續曲線的拐點：

⑴求；

⑵令，解出此方程在區間I內的實根，並求出在區間I內不存在的點；

⑶對於⑵中求出的每一個實根或二階導數不存在的點，檢查在左右兩側鄰近的符號，那麼當兩側的符號相反時，點(,)是拐點，當兩側的符號相同時，點(,)不是拐點。