牟合方蓋
一種用於計算球體體積的方法
《九章算術》的“少廣”章的廿三及廿四兩問中有所謂“開立圓術”,“立圓”的意是“球體”,古稱“丸”,而“開立圓術”即求已知體積的球體的直徑的方法。其中廿四問為:“又有積一萬六千四百四十八億六千六百四十三萬七千五百尺。問為立圓徑幾何?”
開立圓術曰:“置積尺數,以十六乘之,九而一,所得開立方除之,即丸徑。”
從中可知,在《九章算術》內由球體體積求球體直徑,是把球體體積先乘16再除以9,然後再把得數開立方根求出約得14300尺,約為4.76千米,換言之
當然這個結果對數學家而言是極之不滿的,其中為《九章算術》作注的古代中國數學家劉徽便對這公式有所懷疑:
“以周三徑一為圓率,則圓冪傷少;令圓囷為方率,則丸積傷多。互相通補,是以九與十六之率,偶與實相近,而丸猶傷多耳。”
即是說,用來計算圓面積時,則較實際面積要少;若按的比率來計算球和外切直圓柱的體積時,則球的體積又較實際多了一些。然而可以互相通補,但按9:16的比率來計算球和外切立方體體積時,則球的體積較實際多一些。因此,劉徽創造了一個獨特的立體幾何圖形,而希望用這個圖形以求出球體體積公式,稱之為“牟合方蓋”。
是當一正立方體用圓柱從縱橫兩側面作內切圓柱體時,兩圓柱體的公共部分。劉徽在他的注中對“牟合方蓋”有以下的描述:
“取立方棋八枚,皆令立方一寸,積之為立方二寸。規之為圓囷,徑二寸,高二寸。又復橫規之,則其形有似牟合方蓋矣。八棋皆似陽馬,圓然也。按合蓋者,方率也。丸其中,即圓率也。”
其實劉徽是希望構作一個立體圖形,它的每一個橫切面皆是正方形,而且會外接於球體在同一高度的橫切面的圓形,而這個圖形就是“牟合方蓋”,因為劉徽只知道一個圓及它的外接正方形的面積比為,他希望可以用“牟合方蓋”來證實《九章算術》的公式有錯誤。當然他也希望由這方面入手求球體體積的正確公式,因為他知道“牟合方蓋”的體積跟內接球體體積的比為,只要有方法找出“牟合方蓋”的體積便可,可惜,劉徽始終不能解決,他只可以指出解決方法是計算出“外棋”的體積,但由於“外棋”的形狀複雜,所以沒有成功,無奈地只好留待有能之士圖謀解決的方法:
“觀立方之內,合蓋之外,雖衰殺有漸,而多少不掩。判合總結,方圓相纏,濃纖詭互,不可等正。欲陋形措意,懼失正理。敢不闕疑,以俟能言者。”
而賢能之士要在劉徽后二百多年才出現,便是中國偉大數學家袓沖之及他的兒子祖暅,他們承襲了劉徽的想法,利用“牟合方蓋”徹底地解決了球體體積公式的問題。
是到三個“外棋”的計算方法。他們先考慮一個由八個邊長為r的正立方體組成的大正立方體,然後用製作“牟合方蓋”的方法把這大正立方體分割,再取其中一個小正立方體部分作分析,分割的結果將跟右圖所示的相同,白色部分稱為“小牟合方蓋”,它的體積為“牟合方蓋”的八分之一,而紫紅、黃和青色的部分便是三個“外棋”。
祖沖之父子考慮這個小立方體的橫切面。設由小立方體的底至橫切面高度為h,三個“外?”的橫切面面積的總和為S及小牟合方蓋的橫切面邊長為a,因此根據“勾股定理”有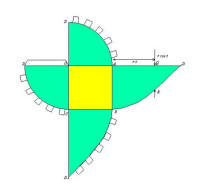

牟合方蓋
另外,因為
所以
於所有的h來說,這個結果也是不變的。祖氏父子便由此出發,他們取一個底方每邊之長和高都等於r的方錐,倒過來立著,與三個“外棋”的體積的和進行比較。設由方錐頂點至方錐截面的高度為h,不難發現對於任何的h,方錐截面面積也必為h²。換句話說,雖然方錐跟三個“外棋”的形狀不同,但因它們的體積都可以用截面面積和高度來計算,而在等高處的截面面積總是相等的,所以它們的體積也就不能不是相等的了,所以祖氏云:
“緣冪勢既同,則積不容異。”
所以
即
因此
這條公式也就是正式的球體體積公式。
雖然本球體體積公式的出現比歐洲阿基米德的公式晚些,但由於方法以至推導都是由劉徽及祖氏父子自行創出,是一項傑出的成就。當中使用的“冪勢既同,則積不容異。”,即“等高處截面面積相等,則二立體的體積相等。”的原理。現在一般認為是由義大利數學家卡瓦列利(Cavalieri)首先引用,稱為卡瓦列利原理(Principle of Cavalieri),但事實上祖氏父子比他早一千年就發現並使用了這個原理,故又稱“祖暅原理”。
