決策空間
決策空間
決策空間亦稱判決空間或行動空間,統計學的基本概念之一。在統計推斷中,根據所抽取的樣本來回答所提出的問題,每一個具體的回答都稱為一個決定或決策(判決、行動)。例如,若問題要估計N(α,σ²)中的參數α,則0.5這個數就是一個決策,它表示“用0.5作為α的估計”這個決定。稱一切可能決策的全體D為決策空間。
決策空間又稱“判定空間”、“判決空間”、“行動空間”。多目標數學規劃模型中可供選擇的全體決策的集合。如方案、措施的總體等。它一般是有限維歐氏空間或無窮維空間的一個子集,往往是凸集。在多目標數學規劃中經常是由一些等式和不等式所界定的集合。多目標數學規劃是在決策空間中尋找使每個目標同時達到最優(帕累托最優)的決策。與單目標的數學規劃(如:線性規劃、非線性規劃)有著本質的不同。多目標數學規劃里的決策空間類似於線性和非線性規劃l中的約束集合。
決策統計量所有可能取值的集合稱為決策空間(decision space),用符號D表示。以閾值 為界,決策空間 分為兩個子空間: ,其中
最後,決策的結果組成結果空間或行為空間(action space)。二元假設檢驗的結果空間由兩個元素 和 組成:
其中 和 分別表示 和 假設檢驗下的決策結果。
決策有硬決策和軟決策之分:如果決策給出的是關於信號有無或者信號屬性(如極性)的判斷,則稱為硬決策。與之不同,如果判斷結果只是某個信號存在或者其屬性的可能性大小(即概率),這便是軟決策。在常見的二元假設檢驗中,通常採用硬決策。
當信號空間 (其中)的元素多於兩個時,稱有關的檢測問題為多元假設檢驗或M元檢測。
綜合以上討論,整個決策理論空間由以下四個子空間組成:
信號或參數空間
觀測樣本空間
決策空間
行為或結果空間
圖1、2、3 以二元檢測問題為例,畫出了決策理論空間的組成。
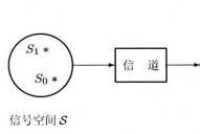
圖1
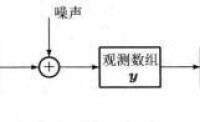
圖2
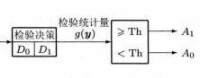
圖3
決策問題有以下三個因素:
(1)狀態空間:自然界或社會所有狀態的全體;
(2)決策空間:決策者所有可能採取決策的全體;
(3)收益函數:自然界或社會處於狀態 時,決策者所採取決策d所獲收益。這種人與自然界或社會的博弈問題稱為決策問題。人們為了更好地作出決策,要從自然界或社會中挖掘各種有用信息。
一般情況下,下面兩種信息對決策起主要作用。
(1)先驗信息。在過去對自然界或社會的各種狀態所獲得的信息。
(2)樣本信息。從與自然界或社會的狀態 有關的環境中去抽樣,從獲得的樣本中了解當今狀態 的最新信息。
如果在一個決策問題中還利用了樣本信息,這種問題稱為統計決策問題。如果在一個統計決策問題中利用了先驗信息,這種問題稱為Bayes決策問題。為了更好地理解統計決策問題,看如下例子。
例 某工廠的產品每100件裝成一箱運交顧客,在向顧客交貨前,面臨如下兩個決策:
:一箱中逐一檢查; :一箱中都不檢查。若工廠選擇決策,則可保證交貨時每件產品都是合格品,但每件產品的檢查費為0.8元,為此,工廠要支付檢查費80元每箱。若工廠選擇決策,則工廠可免付檢查費80元,但顧客發現不合格品時,按照合同規定,不僅更換產品,而且要支付12.5元的賠償費。若一箱中不合格品不超過6件,賠償費不超過75元,則決策如比決策dl有利。若一箱中不合格品超過6件,賠償費不低於87.5元,則決策 比決策 有利。
為了得知一箱中的不合格品率,工廠決定先在每箱中抽取兩件進行檢查,X為其不合格品的件數,根據X的取值,再選擇決策 和。這時工廠的支付費用函數可算得
如何根據抽樣結果和支付費用函數作出決策,使工廠的支付費用最少呢?這是一個典型的統計決策問題。
統計決策的一個基本觀點和假定是每採取一個決策,必然有一定的後果(經濟的或其他的),決策不同,後果各異。對於每個具體的統計決策問題,一般有多種優劣不同的決策可採用。例如,要估計正態分佈 中的參數,假設 的真值為3,那麼採用3.5這個決策顯然比10這個決策好得多。如果要作 的區間估計,則顯然這個決策比這個決策好。統計決策理論的一個基本思想是把上面所談的優劣性以數量的形式表現出來,其方法是引入一個依賴於參數值 和決策 的二元實值非負函數,稱之為損失函數,它表示當參數真值為X而採取決策d時所造成的損失,決策越好,損失就越小。由於在統計問題中人們總是利用樣本對總體進行推斷,所以,誤差是不可避免的,因而總會帶來損失,這就是損失函數定義為非負函數的原因。不同的問題所選擇的損失函數不同。
