雨流計數法
1950年T.Endo等提出的方法
雨流計數法是20世紀50年代由英國的兩位工程師M.Matsuishi和T.Endo提出來的。該計數法的主要功能是把實測載荷歷程簡化為若干個載荷循環,供疲勞壽命估算和編製疲勞試驗載荷譜使用。它以雙參數法為基礎,考慮了動強度(幅值)和靜強度(均值)兩個變數,符合疲勞載荷本身固有的特性。雨流計數法主要用於工程界,特別在疲勞壽命計算中運用非常廣泛。
雨流計數法又可稱為“塔頂法”,是由英國的Matsuiski和Endo 兩位工程師提出的, 距今已有50 多年。雨流計數法主要用於工程界, 特別在疲勞壽命計算中運用非常廣泛。把應變-時間歷程數據記錄轉過90°,時間坐標軸豎直向下, 數據記錄猶如一系列屋面, 雨水順著屋面往下流, 故稱為雨流計數法。雨流計數法對載荷的時間歷程進行計數的過程反映了材料的記憶特性,具有明確的力學概念,因此該方法得到了普遍的認可。
圖13.1
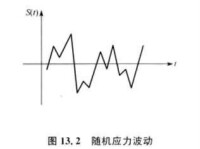
通常測量到的隨機應力S(t)可能由很多峰組成.這給結構承受的循環次數的確定造成了困難。圖13.2所示的是隨機應力數據的一個實例。
雨流計數法簡稱雨流法,也稱寶塔屋頂法。如圖13.3所示,時間軸垂直,隨機應力S(t)代表一系列屋頂,雨流由屋頂流下。
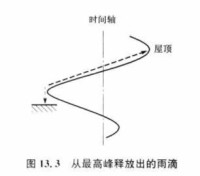
圖13.3
(1)雨流依次從載荷時間歷程的峰值位置的內側沿著斜坡往下流;
(2)雨流從某一個峰值點開始流動,當遇到比其起始峰值更大的峰值時要停止流動;
(3)雨流遇到上面流下的雨流時,必須停止流動;
(4)取出所有的全循環,記下每個循環的幅度;
(5)將第一階段計數后剩下的發散收斂載荷時間歷程等效為一個收斂發散型的載荷時間歷程,進行第二階段的雨流計數。計數循環的總數等於兩個計數階段的計數循環之和。
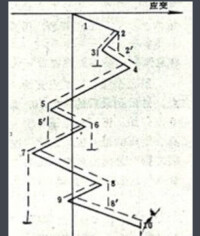
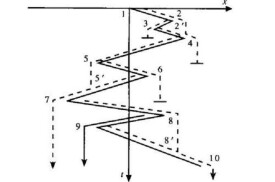
圖1
下一個雨流從峰值4開始,流經5點,豎直下滴到6和7之間的5ˊ點,繼續往下流,再從7點豎直下滴到峰值10的對面,因為10點比4點具有更正的最大值。得出半循環4-5-7。
第五個流動從5點開始,流到6點,豎直下滴,終止於7點的對面,因為7點比5點具有更負的極小值。取出半循環5-6。第六個流動從6點開始,因為遇到由5點滴下的雨滴,所以流到5ˊ點終止。半循環6-5與5-6配成一個完全循環5ˊ-6-5,取出5ˊ-6-5。
第七個流動從7點開始,經過8點,下落到9-10線上的8ˊ點,然後到最後的峰值10,取出半循環7-8-10。第八個流動從8點開始,流至9點下降到10點的對面終止,因為10點比8點具有更正的最大值。取出半循環8-9。最後一個流動從9點開始,因為遇到由8點下滴的雨流,所以終止於8ˊ點。取出半循環9-8ˊ。把兩個半循環8-9和9-8ˊ配對,組成一個完全的循環8-9-8ˊ。
這樣,圖1所示的應變一時間記錄包括三個完全循環8-9-8ˊ,2-3-2ˊ,5-6-5ˊ和三個半循環1-2-4,4-5-7,7-8-10。圖1表明,雨流法得到的應變是與材料應力-應變特性相一致的。從圖1中看出,有三個完全的循環,與此對應,在圖2中有三個陰影線所示的閉合迴路。
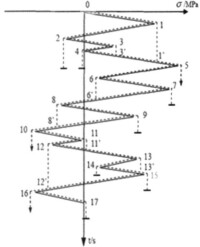
圖2