槓桿原理
槓桿受力平衡原理
槓桿原理也稱為“槓桿平衡條件”，是分析槓桿受力平衡的定理，最早由古希臘科學家阿基米德提出。槓桿要達到受力平衡，作用在槓桿上的兩個力矩（力與力臂的乘積）必須大小相等，旋轉方向相反。也就是說，槓桿的平衡條件必須滿足：動力×動力臂必須等於阻力×阻力臂，數學表達式為：F1·L1=F2·L2。式中，F1表示動力，L1表示動力臂，F2表示阻力，L2表示阻力臂。
槓桿原理槓桿又分稱費力槓桿、省力槓桿和等臂槓桿。
古希臘科學家阿基米德最早在《論平面圖形的平衡》一書中提出了槓桿原理。他曾有一句廣為流傳的名言：“給我一個支點，我就能撬起整個地球！”，這句話說的便是槓桿原理。
在槓桿原理提出之前，阿基米德先把槓桿實際中的一些經驗知識當作“不證自明的公理”，這些公理包括
1）在無重量的桿的兩端離支點相等的距離處掛上相等的重量，它們將平衡；
2）在無重量的桿的兩端離支點相等的距離處掛上不相等的重量，重的一端將下傾；
3）在無重量的桿的兩端離支點不相等距離處掛上相等重量，距離遠的一端將下 傾；
4）一個重物的作用可以用幾個均勻分佈的重物的作用來代替，只要重心的位置保持不變。相反，幾個均勻分佈的重物可以用一個懸掛在它們的重心處的重物來代替
5）相似圖形的重心以相似的方式分佈……
然後，基於這些公理，他運用嚴謹的幾何學及邏輯論，提出了槓桿原理。阿基米德 r認為，二重物平衡時，它們離支點的距離與重量成反比。
阿基米德除了對槓桿進行研究理論外，還將該原理付諸於實踐。據說，他曾藉助槓桿和滑輪組，使停放在沙灘上的船隻順利下水；在保衛敘拉古免受羅馬海軍襲擊的戰鬥中，他利用槓桿原理製造了遠、近距離的投石器，發射出各種飛彈和巨石攻擊敵人，曾把羅馬人阻於敘拉古城外達3年之久。
我國戰國時期的墨子也曾對槓桿進行過探究。據《墨子 · 經說下》記載：“衡，加重於其一旁，必捶，權重相若也。相衡，則本短標長。兩加焉重相若，則標必下，標得權也”。這兩條對槓桿的平衡說得很全面。裡面有等臂的，有不等臂的；有改變兩端重量使它偏動的，也有改變兩臂長度使它偏動的。
使用槓桿時，為了省力，就應該用動力臂比阻力臂長的槓桿；如果想要省距離，就應該用動力臂比阻力臂短的槓桿。因此使用槓桿可以省力，也可以省距離。但是，要想省力，就必須多移動距離；要想少移動距離，就必須多費些力。要想又省力而又少移動距離，是不可能實現的。
槓桿的支點不一定要在中間，滿足以下三個點的系統，基本上就是槓桿：支點、施力點、受力點。
其中，力矩平衡公式這樣寫：動力×動力臂=阻力×阻力臂，即F1×L1=F2×L2。這就是一個槓桿。
動力臂延伸
槓桿有省力槓桿，也有費力槓桿，兩者功能表現有所不同。例如腳踩的打氣機，手壓的榨汁機，就是省力槓桿 (動力臂 > 阻力臂）；儘管省力了，但我們卻要壓下較大的距離，受力端只有較小的動作。另有一種是費力槓桿。例如路邊的吊車，釣東西的鉤子在整個桿的尖端，尾端是支點、中間是油壓機 (力矩 > 力臂），這就是費力的槓桿。但費力換來的是中間的施力點只要動小距離，尖端的掛勾就會移動相當大的距離。
兩種槓桿都有用處，不同的應用場景需要評估是要省力或是省下動作範圍。另外，有種機械叫輪軸，也可當作是一種槓桿的應用，只是表現上有時需要增加轉動的計算。
阿基米德的名言："假如給我一個支點，就能撬起地球！"不僅催人奮進，更有著嚴謹的科學根據。
槓桿平衡是指槓桿在動力和阻力作用下處於靜止狀態下或者勻速轉動的狀態下。槓桿受力通常有兩種情況。
1）槓桿上受兩個力作用時
動力×支點到動力作用線的距離=阻力×支點到阻力作用線的距離，即動力×動力臂=阻力×阻力臂，代數式表示為F1×L1=F2×L2
2）槓桿上受多個力作用時
所有使槓桿順時針轉動的力的大小與其對應力臂的乘積等於使槓桿逆時針轉動的力的大小與其對應力臂的乘積。這也叫作槓桿的順逆原則，同樣適用於只受兩個力作用的情況。
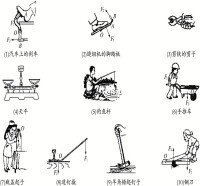
槓桿的分類
L1>L2,F1
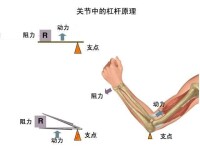幾乎每一台機器中都少不了槓桿，人體中也有許多的槓桿在起作用。譬如，拿起一件東西，彎一下腰，甚至翹一下腳尖都是人體的槓桿在起作用，了解了人體的槓桿不僅可以增長物理知識，還能學會許多生理知識。
日常拔釘子用的羊角錘、鍘刀，開瓶器，軋刀，動滑輪，手推車 剪鐵皮用的剪刀及剪鋼筋用的剪刀等。
L1F2,費力、省距離。
如釣魚竿、鑷子，筷子，船槳裁縫用的剪刀 理髮師用的剪刀等。
L1=L2,F1=F2,既不省力也不費力，又不多移動距離，
如天平、定滑輪等。
費力槓桿
人體中大部分槓桿為費力槓桿，也有小部分是等臂和省力槓桿。
點一下頭或抬一下頭是靠槓桿的作用，槓桿的支點在脊柱之頂，支點前後各有肌肉，頭顱的重量是阻力。支點前後的肌肉配合起來，有的收縮有的拉長配合起來形成低頭仰頭。
當曲肘把重物舉起來的時候，手臂也是一個槓桿。肘關節是支點，支點左右都有肌肉。這是一種費力槓桿，舉起一份的重量，肌肉要花費6倍以上的力氣，雖然費力，但是可以省一定距離。
當你把腳尖翹起來的時候，是腳跟後面的肌肉在起作用，腳尖是支點，體重落在兩者之間。這是一個省力槓桿，肌肉的拉力比體重要小。而且腳越長越省力。
如果你彎一下腰，肌肉就要付出接近1200牛頓的力量。這是 由於在腰部肌肉和脊骨之間形成的槓桿也是一個費力槓桿。所以在彎腰提起立物時，正確的姿式是盡量使重物離身體近一些，以避免肌肉被拉傷。
阿基米德將自己鎖在一間小屋裡，夜以繼日地埋頭寫作《浮體論》。這天，一位朝臣突然闖進來，一進門就喊道：“原來您躲在這裡。國王正調動人馬四處找你呢。阿基米德心想：外面一定出大事了。他立即收拾起書稿，隨大臣一同出去，直奔王宮。
當他們來到宮殿前，看見衛兵們銀槍鐵盔，殿內文武滿座，國王正焦急地在地毯上來回踱步，宮殿內的長條案上擺著海防圖、陸防圖。阿基米德知道，他最擔心的戰爭終於爆發了。
原來地中海沿岸的羅馬王朝和迦太基連年征戰，雙方互有勝負。敘拉古是夾在迦、羅兩個強國中的城邦小國，常常隨著兩個強國的勝負而棄弱附強，飄忽不定。阿基米德對這種外交策略很不放心，曾多次告誡國王，不要惹禍上身。可是敘拉古的國王年少無知，剛愎自用，惹惱了羅馬人。現在打了勝仗的羅馬人決定從海陸兩路進攻敘拉古，國王嚇得沒了主意。當他看到阿基米德來了，連忙懇求道：“親愛的阿基米德，你是最聰明的人，先王在世時說過你都能推動地球。”
關於阿基米德推動地球的說法，要追溯到他在亞歷山大里亞留學。當時，他從埃及農民提水用的吊杆和奴隸們撬石頭用的撬棍受到啟發，發現可以藉助槓桿來達到省力的目的，而且發現，手握的地方到支點的這一段距離越長，就越省力氣。由此他提出了這樣一個定理：力臂和力（重量）的關係成反比例。這就是槓桿原理。用現在的表達方式表述就是：動力×動力臂=阻力×阻力臂。為此，他曾給當時的國王亥尼洛寫信說： `我不費吹灰之力，就可以隨便移動任何重量的東西；只要給我一個支點，給我一根足夠長的槓桿，我連地球都可以推動。'
可現在的國王並不懂得什麼叫科學，他只知道大難臨頭了，希望阿基米德能夠救駕。
可是羅馬軍隊實在太厲害了，四個羅馬陸軍軍團已經挺進到了敘拉古城的西北，城外鼓聲齊鳴，殺聲震天。危急關頭，阿基米德說到：“如果單靠實力，我們決不是羅馬人對手。現在若能造出一種新式武器來，或許還可守住城池，以待援兵。”國王一聽這話，立即轉憂為喜，讓阿基米德全權指揮這場守衛戰。
兩天後，整齊的羅馬軍團方陣向護城河攻來。突然，城裡隱約傳來吱呀的響聲，接著城頭上飛出大大小小的石塊，山洪般地傾瀉下來。羅馬人漸漸支持不住了，連滾帶爬地四散逃命。
阿基米德到底造出了什麼秘密武器讓羅馬人大敗而歸呢? 原來他製造出了特大的弩弓—投石機。這是一種巨大的弓，人是根本拉不動的，他利用了槓桿原理。只要將弩上轉軸的搖柄用力扳動，那與搖柄相連的牛筋又拉緊許多根牛筋組成的粗弓弦，拉到最緊時，再突然一放，弓弦就帶動載石裝置，把石頭高高地拋出城外。原來這槓桿原理並不是簡單使用一根直棍撬東西。
擊敗從西北攻城的羅馬陸軍軍團之後，又有戰報傳來，羅馬海軍從東南海面上發動了攻勢。當羅馬戰船開到敘拉古城下，士兵們拿著雲梯正要往牆上搭的時候，突然城頭上伸出了幾副木頭架子，木架上垂下一條條鐵鏈，鏈頭上有鐵鉤、鐵爪，鉤住了羅馬海軍的戰船。任水兵們怎樣使勁划槳，用刀砍，用火燒，大鐵鏈分毫無損，戰船不能挪動半步。正當船上一片驚慌時，只見大木架上的木輪又“嘎嘎”地轉動起來，鐵鏈越拉越緊，船漸漸地被吊起離開了水面。隨著船身的傾斜，士兵們紛紛掉進了海里，桅杆也被折斷了……阿基米德的這些"怪物"原來也是利用了槓桿原理，並加了滑輪。
“給我一個支點，我就能撬起地球！”，這是古代發現槓桿原理的阿基米德說的話。阿基米德知道，如果利用槓桿，就能用一個很小的力，把非常重的東西舉起來，只要把這個力放在槓桿的長臂上，而讓短臂對重物起作用。
然而如果這個古代偉大科學家知道了地球的質量，他也許就不會這樣誇口了。讓我們設想阿基米德真的找到了另一個地球做支點；再設想他也做成了一根夠長的槓桿。你知道他得用多少時間才能把質量等於地球的一個重物舉起，哪怕只舉起1cm呢？至少要30萬億年！
地球的質量到底有多大呢？大約是：kg。
如果一個人只能直接舉起60kg的重物，那麼他要“舉起地球”，就得把自己的手放在一根這樣長的槓桿上，他的長臂應當等於它的短臂的倍。
簡單地計算一下就可以知道，在短臂的那一頭舉高1cm，就得在長臂那一頭在宇宙空間里畫一個大弧形，弧的長度大約是：m。
這就是說，阿基米德如果要把地球舉起1cm，他那扶著槓桿的手就得移動大到這樣不可想象的一個距離！那麼他要用多少時間才能做完這件事呢？如果我們認為阿基米德能在一秒中里把60kg的重物舉高一米（這種工作能力已經幾乎等於一馬力！），那麼，他要把地球舉起1cm，就得用去 秒，即三萬億年！可見阿基米德根本無法完成這個任務。
關於撬起地球還有另一種解讀，阿基米德說的是撬起地球，而不是說撬起地球1cm。他在長槓桿的另一頭，只需要撬動1m，相應的地球也會移動m，地球移動的距離可能很短很短，但是不管如何，地球還是動了。
目錄