有限自動機
有限自動機
有限自動機(finite automata)亦稱時序機,有限離散數字系統的抽象數學模型。一個有限自動機M由五元組(X,Y,S,δ,λ)給定,其中X,Y和S都是非空有限集,分別稱為M的輸入集、輸出集和狀態集;δ是笛卡兒積集合S×X到S的映射,稱為M的下一狀態函數;λ是S×X到Y的單值映射,稱為M的輸出函數。當δ是單值映射時,稱M為確定型有限自動機;當δ是多值映射時,稱M為非確定型有限自動機。有限自動機有三種功能:作為序列轉換器,將輸入序列變換為輸出序列;作為序列識別器,識別輸入的序列是否具有某種性質;作為序列產生器,產生具有所要求性質的序列。
有限自動機(finite automata)或稱為有窮狀態的機器,它由一個有限的內部狀態集和一組控制規則組成,這些規則是用來控制在當前狀態下讀入輸入符號后應轉向什麼狀態。有限狀態系統最初的形式研究是在1943年南McCulloeh和Pitts提出來的,有限自動機是一種數學模型,它可以用來描述識別輸入符號串的過程,在這個機器中,它的狀態總是處於有限狀態中的某一個狀態,系統的當前狀態概括了有關歷史的信息,這些歷史信息對於後來的輸入所能確定的系統狀態是不可少的。簡單地說,也就是要根據當前系統的狀態和下一個輸人的符號才能確定下一個狀態。例如電梯的控制機構是有限自動機的一個例子,顧客的服務要求(即所要到達的樓層)是該裝置的輸入信息,而電梯所處的層數及運動方向則表示該裝置的狀態,這個機構並不記住所有先前服務要求,而僅僅記住是在幾樓,運動的方向(上或下)及尚未滿足的服務要求,在計算機科學中,可以找到許多有限狀態系統的例子,如計算機本身也可以是認為是一個有限狀態系統,儘管其可能狀態數目很大,但仍然是有限的,有限自動機理論是設計這些系統的有效工具,研究有限狀態系統的重要原因是概念的自然性和應用的廣泛性,例如,在編譯器中,人們主要用自動機來識別程序設計語言中的單詞,但是它不能用來描述表達式、語句等複雜的語法結構。
有限自動機與正規文法和正規式有著非常密切的關係,它們的描述能力是相同的,因此,有限自動機是用來識別正規式的一個非常有用的工具,使用有限自動機來構造詞法分析程序這也是一種比較好的途徑。
定義1一個確定有限自動機(DFA)M是一個五元組
其中,
∑是一個有窮字母表,它的每一個元素稱為一個輸入符號;
S是一個有限狀態集,它的每一個元素稱為一個狀態;
f是轉換函數,定義了從 上的一個單值映射,即 ,指明當前的狀態為p,當輸入符號為a時,則轉換到下一個狀態q,q稱為p的後繼狀態;
是一個唯一的初始狀態;
是一個終止狀態集。
在狀態轉移的每一步,根據有限自動機當前所處的狀態和所面臨的輸入符號,便能唯一地確定有限自動機的下一個狀態,即轉換函數的值是唯一的,反映到狀態轉換圖上,就是若 ,則任何結點的出邊都有n條,且這些出邊上的標記均不相同,這就是為什麼我們把按上述方式定義的有限自動機稱為確定的有限自動機的原因。
定義2 DFAM所接受的符號串的集合稱為DFAM所接受的語言,記為L(M),即
換句話說,對於中的任何一個串虯w,若存在一條從某一表示初態的結點到某一表示終態結點的通路,且這條路上所有弧的標記符依次連接成的符號串等於w,則稱w可為DFAM所識別(讀出或接受)。
若有限自動機根據當前所處的狀態和所面臨的輸入符號,能夠確定的後繼狀態不是唯一的,就稱這樣的有限自動機為不確定的有限自動機。如圖1是NFA,在這個NFA中,狀態0在輸入符號a時有兩個可能的轉移狀態0,1。
我們一定已經注意到前述的DFA只是NFA的一種特殊情況,對於給定的輸入字元串w和狀態,在DFA中,恰好存在始於標記為w,的一條路徑,而在NFA中,卻可能存在始於,標記為w的若干條路徑。
下面給出不確定有限自動機的形式定義如下:
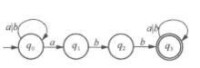
圖1
其中,
是一個有窮字母表,它的每一個元素稱為一個輸入符號;
S是一個有限狀態集,它的每一個元素稱為一個狀態;
f是轉換函數,定義了從 上的映射 ( 表示S的冪集),即 ,指明當前的狀態為p,當輸入符號為a時,則轉換到的狀態是一個狀態集;
是的初始狀態集;
是一個終止狀態集。
從NFA的定義可以看到,NFA與DFA的主要的區別在於轉換函數,DFA的轉換函數是從到S上的一個單值映射,而NFA的轉換函數是從到 ,即S的冪集的映射,而不是到S的映射,即一個狀態可轉換到的後繼狀態是一個狀態集合(可能是空集),而不是單個狀態。另外,NFA有一個初態集,而DFA的初態是唯一的。
研究有限自動機的功能、結構以及兩者關係的數學理論稱為有限自動機理論,有限自動機理論的基本內容包括邏輯網路、狀態化簡、狀態分配、神經網路和有限識別器等。
基本的邏輯元件按是否具有記憶功能,可以分為記憶元件(如觸發器和延遲器等)和組合元件(如各種與、或、非門等)兩類,把一些基本邏輯元件按一定要求連結起來,就組成邏輯網路,若把邏輯網路中進入記憶元件的輸入線去掉后所得網路不再含有迴路,則稱這樣的網路為合式網路,不含記憶元件的合式網路稱組合網路,邏輯網路比組合網路複雜,在工程實現上,要求對於一個給定的有限自動機建立和實現此有限自動機的邏輯網路,已經證明任何合式網路的功能都可以用一個有限自動機來描述;任何一個有限自動機描述的功能也都可以用合式網路來實現。
對任何有限自動機都惟一(在同構意義下)存在一個狀態數目最少的有限自動機與它等價,根據有限自動機理論,對給定的有限自動機,可有效地求出與之等價的最簡形式的有限自動機。
要構造具有多個狀態的網路,需要使用多個基本記憶元件,利用這些記憶元件的各種狀態組合來表示不同的狀態。一般地,不同的狀態分配導致邏輯網路具有不同的複雜程度,如何選擇較好的分配方案,使邏輯網路的構造儘可能地簡單,是有限自動機研究的一個主要課題。
1943年,麥克卡洛克(Mcculloch)和皮特斯(Pitts,W.)提出的神經網路模型是有限自動機的一個實例,1951年,克林(Kleene,S.C.)在這種神經網路模型的基礎上,提出了正則事件(正則語法)的概念,證明了正則事件是可以被神經網路或有限自動機表示的事件,而且神經網路或有限自動機可以表示的事件也一定是正則事件。
在形式語言理論中,有限自動機通常作為語言的識別器來使用,作為識別器,有限自動機的輸出可以被忽略,而由最後達到的狀態去決定輸入序列是否具有給定的性質,這種有限自動機也稱為有限接收機,按其下步狀態是否完全確定,有限識別器可分為確定型和非確定型兩種,它們分別與確定型和非確定型有限自動機相對應,它們也都接受同一類語言,即正則語言。