正稜錐
稜錐的種類之一
正稜錐是指一個稜錐的底面是正多邊形,且頂點在底面的射影是底面的中心的稜錐。側棱與底面邊長相等的正三稜錐叫做正四面體。
正稜錐的體積:如果正稜錐的底面積為S,頂點到底面的距離為h,則V=1/3Sh。
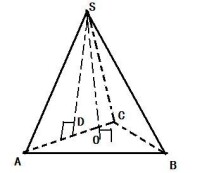
正稜錐
(2)正稜錐的高、斜高和斜高在底面內的射影組成一個直角三角形,正稜錐的高、側棱、側棱在底面內的射影也組成一個直角三角形;
(3)正稜錐的側棱與底面所成的角都相等;正稜錐的側面與底面所成的二面角都相等;
(4)正稜錐的側面積:如果正稜錐的底面周長為c,斜高為h’,那麼它的側面積是。
(5)正稜錐的體積:如果正稜錐的底面積為S,頂點到底面的距離為h,則
正稜錐的側面展開圖是由公共頂點的若干個等腰三角形三角形所組成的平面圖形。等腰三角形的腰是正稜錐的側棱長。它的底就是正稜錐的底面邊長。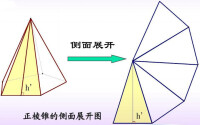

正稜錐
圖二是正三稜錐、正四稜錐、正五稜錐、正六稜錐的展開圖。此外尚有多種展開方法。正四面體是正三稜錐圖二的特例。如圖所示,正稜錐(正多稜錐)的底面是正多邊形,側面全是等腰三角形。
隨著稜錐的高度以及底面正多邊形大小的不同,其側面的等腰三角形的形狀也各有差異。例如,正三稜錐的3個側面構成了3個全等的等腰三角形,正四稜錐的4個側面構成4個全等的等腰三角形。
另外,正五稜錐、正六稜錐……,也各自構成5個、6個……全等的等腰三角形。
如圖二所示,實線部分為切割線,若從虛線處摺疊,即可製成正稜錐。
從正稜錐的頂點向底面引垂線,該垂線定會通過底面正多邊形的中心。
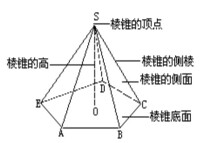
正稜錐
畫法:
(1)畫軸。畫x′軸、y′軸、z′軸,記坐標原點為O′,使(或135°),。
(2)畫底面。按x′軸、y′軸畫正五邊形的直觀圖ABCDE,按比例尺取邊長等於,並使正五邊形的中心對應於點O′。
(3)畫高線。在z′軸取
(4)成圖。連結,並加以整理(去掉輔助線,將被遮擋的部分改為虛線),就得到所畫的正五稜錐的直觀圖。
