滅點
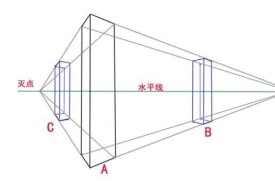
多條平行線延伸至遠處的聚合點
滅點線性透視中,兩條或多條代表平行線線條向遠處地平線(HORIZON LINE)伸展直至聚合的那一點。現實中平行的線能在滅點上推進而聚合的原則同樣是以肉眼觀察到的現象為依據的,如鐵路的兩條路軌看上去確實像在地平線上匯合到了一起。畫面中可有一個或多個滅點,這取決於構圖的座標位置和方向;所有的滅點可能都落在地平線上,或在畫平面(PICTURE PLANE)外的延伸線上。按斜角透視(OBLIQUE PERSPECTIVE),即以鳥瞰法(BIRD'S-EYE VIEW)或蟲視法(WORM'S EYE VIEW)角度拉伸繪製的長方體有三個滅點,其中一個不在地平線上,而是在地平線之下(鳥瞰法)或之上(蟲視法)。又稱“消失點”。
滅點:在透視投影中,一束平行於投影面的平行線的投影可以保持平行,而不平行於投影面的平行線的投影會聚集到一個點,這個點成為滅點(Vanishing Point)。滅點可以看作是無限遠處的一點在投影面上的投影。
滅點
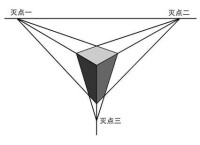
2.如果是成角透視,有兩個滅點,在對象的兩側的後方。方法是分別延長物體左右兩方的有會聚趨勢的四條線,兩兩交於對象左右兩邊的後方。形成兩個滅點。成角透視是最符合視覺習慣的透視。很富有立體感。凡是平行於畫面的直線都沒有滅點,凡是與畫面有一定角度的一組平行線,都有滅點。如果這個角度是90度,就是平行透視。否則是成角透視。
影滅點——正面自然光照射,陰影向後的消失點。標識為VS(Vanishingofshadow),光滅點——影滅點向下垂直於觸影面的點。標識為VL(Vanishingoflight)。
一條直線的滅點是過攝影中心且平行於該直線的直線與像平面的交點。
推論1:位於空間中一個平面內的直線的滅點,是過投影中心且與該平面平行的平面與像平面的交線。
推論2:空間中與某平面平行的直線的滅點在一條直線上。